题目内容
【题目】如图,已知AB∥CD,CE,BE的交点为E,现作如下操作:
第一次操作,分别作∠ABE和∠DCE的平分线,交点为E1,
第二次操作,分别作∠ABE1和∠DCE1的平分线,交点为E2,
第三次操作,分别作∠ABE2和∠DCE2的平分线,交点为E3……
第n次操作,分别作∠ABEn-1和∠DCEn-1的平分线,交点为En.
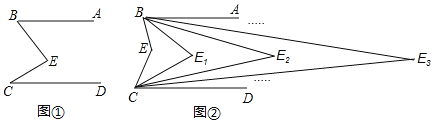
(1)如图①,求证:∠E=∠B+∠C;
(2)如图②,求证:∠E1=![]() ∠E;
∠E;
(3)猜想:若∠En=b°,求∠BEC的度数.
【答案】(1)证明见解析;(2)证明见解析;(3)∠BEC=2nb°.
【解析】试题分析:(1)先过E作EF∥AB,根据AB∥CD,得出AB∥EF∥CD,再根据平行线的性质,得出∠B=∠1,∠C=∠2,进而得到∠BEC=∠ABE+∠DCE;
(2)先根据∠ABE和∠DCE的平分线交点为E1,运用(1)中的结论,得出∠CE1B=∠ABE1+∠DCE1= ![]() ∠ABE+
∠ABE+![]() ∠DCE=
∠DCE=![]() ∠BEC;同理可得∠BE2C=∠ABE2+∠DCE2=
∠BEC;同理可得∠BE2C=∠ABE2+∠DCE2=![]() ∠ABE1+
∠ABE1+![]() ∠DCE1=
∠DCE1=![]() ∠CE1B=
∠CE1B=![]() ∠BEC;
∠BEC;
(3)根据∠ABE2和∠DCE2的平分线,交点为E3,得出∠BE3C=![]() ∠BEC;…据此得到规律∠En=
∠BEC;…据此得到规律∠En=![]() ∠BEC,最后求得∠BEC的度数.
∠BEC,最后求得∠BEC的度数.
试题解析:(1)如图①,过E作EF∥AB,
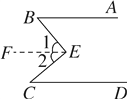
∵AB∥CD,
∴AB∥EF∥CD,
∴∠B=∠1,∠C=∠2,
∵∠BEC=∠1+∠2,
∴∠BEC=∠ABE+∠DCE;
(2)如图2,∵∠ABE和∠DCE的平分线交点为E1,

∴由(1)可得,
∠CE1B=∠ABE1+∠DCE1=![]() ∠ABE+
∠ABE+![]() ∠DCE=
∠DCE=![]() ∠BEC;
∠BEC;
∵∠ABE1和∠DCE1的平分线交点为E2,
∴由(1)可得,
∠BE2C=∠ABE2+∠DCE2=![]() ∠ABE1+
∠ABE1+![]() ∠DCE1=
∠DCE1=![]() ∠CE1B=
∠CE1B=![]() ∠BEC;
∠BEC;
(3)如图2,∵∠ABE2和∠DCE2的平分线,交点为E3,
∴∠BE3C=∠ABE3+∠DCE3=![]() ∠ABE2+
∠ABE2+![]() ∠DCE2=
∠DCE2=![]() ∠CE2B=
∠CE2B=![]() ∠BEC;
∠BEC;
…
以此类推,∠En=![]() ∠BEC,
∠BEC,
∴当∠En=α度时,∠BEC等于2nα度.







