题目内容
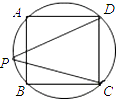
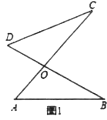
【题目】小学我们已经知道三角形三个内角和是180°,对于如图1中,![]() ,
,![]() 交于
交于![]() 点,形成的两个三角形中的角存在以下关系:①
点,形成的两个三角形中的角存在以下关系:①![]() ;②
;②![]() .试探究下面问题:
.试探究下面问题:
已知![]() 的平分线
的平分线![]() 与
与![]() 的平分线
的平分线![]() 交于点
交于点![]() ,
,
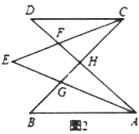
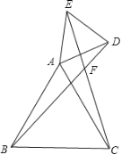
(1)如图2,若![]() ,
,![]() ,
,![]() ,则
,则![]() _________;
_________;
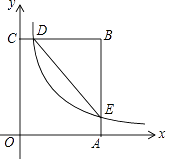
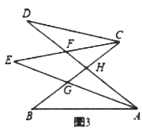
(2)如图3,若![]() 不平行
不平行![]() ,
,![]() ,
,![]() ,则
,则![]() _______.
_______.
(3)在总结前两问的基础上,借助图3,探究![]() 与
与![]() 、
、![]() 之间是否存在某种等量关系?若存在,请说明理由;若不存在,请举例说明.
之间是否存在某种等量关系?若存在,请说明理由;若不存在,请举例说明.
【答案】(1)35°;(2)40°;(3)∠D+∠B=2∠E,理由见解析
【解析】
(1)(2)在△CDF和△AEF中,有:∠D+∠DCF= ∠E+∠DAE①;在△ABG和△CEG中, ∠B+∠EAB= ∠E+∠BCE②;①+②再结合![]() 的平分线
的平分线![]() 与
与![]() 的平分线
的平分线![]() 交于点
交于点![]() ,进行化简得到∠E=
,进行化简得到∠E=![]() (∠B+∠D),然后将∠B和∠D代入即可解答;
(∠B+∠D),然后将∠B和∠D代入即可解答;
(3)根据(1)(2)的推导即可得到∠D+∠B=2∠E.
解:(1)如图2在△CDF和△AEF中,有∠D+∠DCF= ∠E+∠DAE①
△ABG和△CEG中, 有∠B+∠EAB= ∠E+∠BCE②
①+②得:∠D+∠DCF+∠B+∠EAB=∠E+∠DAE+∠E+∠BCE
又∵![]() 的平分线
的平分线![]() 与
与![]() 的平分线
的平分线![]() 交于点
交于点![]()
∴∠DCF=∠BCE,∠EAB=∠DAE
∴∠E=![]() (∠B+∠D)
(∠B+∠D)
∵![]() ,
,![]()
∴∠E=35°
(2)如图3:同(1)可得∠E=![]() (∠B+∠D)
(∠B+∠D)
∵![]() ,
,![]()
∴∠E=40°
(3)解:∠D+∠B=2∠E.
理由如下:
在△CDF和△AEF中,有∠D+∠DCF= ∠E+∠DAE①
△ABG和△CEG中, 有∠B+∠EAB= ∠E+∠BCE②
①+②得:∠D+∠DCF+∠B+∠EAB=∠E+∠DAE+∠E+∠BCE
又∵![]() 的平分线
的平分线![]() 与
与![]() 的平分线
的平分线![]() 交于点
交于点![]()
∴∠DCF=∠BCE,∠EAB=∠DAE
∴∠E=![]() (∠B+∠D)
(∠B+∠D)
∴∠D+∠B=2∠E

练习册系列答案
相关题目