题目内容
下列结论正确的是( )
| A、x-3=1的解是x=-2 | ||||
| B、2-x=1的解是x=1 | ||||
C、x=-
| ||||
D、-
|
分析:方程的解就是能够使方程两边左右相等的未知数的值,即利用方程的解代替未知数,所得到的式子左右两边相等.
解答:解:A、把x=-2代入x-3=1,左边=-2-3=-5,左边≠右边,因而x=-2不是方程x-3=1的解.
B、把x=1代入2-x=1,左边=2-1=1,左边=右边,因而2-x=1的解是x=1.
C、把x=-
代入-
x=3,左边=(-
)×(-
)=
,右边=3,左边≠右边,因而x=-
不是方程-
x=3的解.
D、把x=-1代入方程-
x=
,左边=
,左边≠右边,因而-
x=
的解不是x=-1.
故选B.
B、把x=1代入2-x=1,左边=2-1=1,左边=右边,因而2-x=1的解是x=1.
C、把x=-
| 3 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| 2 |
| 3 |
| 4 |
| 3 |
| 2 |
| 1 |
| 2 |
D、把x=-1代入方程-
| 2 |
| 3 |
| 3 |
| 2 |
| 2 |
| 3 |
| 2 |
| 3 |
| 3 |
| 2 |
故选B.
点评:本题主要考查了方程解的定义,及判断一个数是否是方程的解的方法.

练习册系列答案
相关题目
下列结论正确的是( )
A、
| ||
B、当x=-3时,分式
| ||
| C、(-a+b)(-a-b)=a2-b2 | ||
| D、a2+a3=a5 |
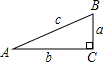 如图,在Rt△ABC中,∠C=90°,BC=a,CA=b,AB=C,则下列结论正确的是( )
如图,在Rt△ABC中,∠C=90°,BC=a,CA=b,AB=C,则下列结论正确的是( )A、sinB=
| ||
B、cosB=
| ||
C、tanB=
| ||
D、cotB=
|
如果-b是a的立方根(ab≠0),那么下列结论正确的是( )
| A、-b也是-a的立方根 | B、b是a的立方根 | C、b是-a的立方根 | D、以上结论均不正确 |
