题目内容
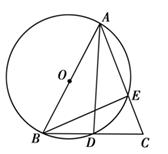
如图,在△ABC中,AB=AC,以AB为直径的⊙O交AC与E,交BC与D.求证:
小题1: 是
是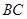 的中点;(
的中点;(
小题2:△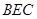 ∽△
∽△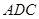 ;
;
小题3: 。
。

小题1:
 是
是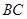 的中点;(
的中点;(小题2:△
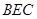 ∽△
∽△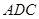 ;
;小题3:
 。
。小题1:证明:∵AB是⊙O的直径,∴∠ADB="90°" ,
|
∴D是BC的中点;
小题2:证明:∵∠CBE与∠CAD是同弧所对的圆周角,
∴∠CBE=∠CAD.
又∵∠BCE=∠ACD,
∴△BEC∽△ADC;
小题3:证明:由△BEC∽△ADC,知
 ,
,即CD·BC=AC·CE.
∵D是BC的中点,∴CD=
 BC.
BC.又∵AB=AC,∴CD·BC=AC·CE=
 BC·BC=AB·CE
BC·BC=AB·CE即BC
 =2AB·CE.
=2AB·CE. 略

练习册系列答案
相关题目

 =
= ;③AC?BE=12;④3BF=4AC.其中结论正确的个数有( )
;③AC?BE=12;④3BF=4AC.其中结论正确的个数有( )