Question

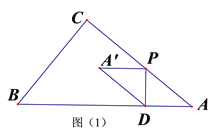
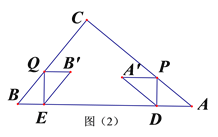
【题目】如图△ABC 的∠ABC 的外角平分线 BD 与∠ACB 的外角平分线 CE 交于 P，过 P 作 MN∥AB 交 AC 于M，交 BC 于 N，且 AM＝8，BN＝5，则 MN＝（ ）

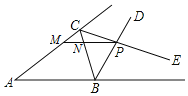
A. 2B. 3C. 4D. 5

Answer 1

【答案】B

【解析】

过P作PF⊥AC，PG⊥BC，PH⊥AB，连接AP，依据条件可得AP平分∠BAC，再根据平行线的性质和角平分线定义得出∠MAP=∠MPA，∠NBP=∠NPB，即可得到AM=PM，NP=NB，再根据MN=MP-NP=AM-BN进行计算即可．

如图，过P作PF⊥AC，PG⊥BC，PH⊥AB，连接AP，

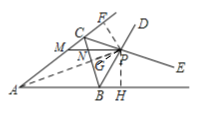
∵∠ABC的外角平分线BD与∠ACB的外角平分线CE交于P，
∴PF=PG=PH，
∴点P在∠BAC的平分线上，即AP平分∠BAC，
∴∠MAP=∠BAP，
∵MN∥AB，
∴∠BAP=∠MPA，
∴∠MAP=∠MPA，
∴AM=PM，
同理可得：∠NBP=∠NPB，
∴NP=NB，
∴MN=MP-NP=AM-BN=8-5=3，
故选：B．