题目内容
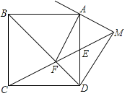
【题目】如图![]() ,点
,点![]() 将线段
将线段![]() 分成两部分,如果
分成两部分,如果![]() ,那么称点
,那么称点![]() 为线段
为线段![]() 的黄金分割点.
的黄金分割点.
![]() 某研究小组在进行课题学习时,类似地给出“黄金分割线”的定义:直线
某研究小组在进行课题学习时,类似地给出“黄金分割线”的定义:直线![]() 将一个面积为
将一个面积为![]() 的图形分成两部分,这两部分的面积分别为
的图形分成两部分,这两部分的面积分别为![]() ,
,![]() ,如果
,如果![]() ,那么称直线
,那么称直线![]() 为该图形的黄金分割线.(如图
为该图形的黄金分割线.(如图![]() )
)
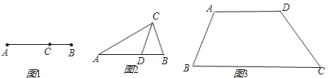
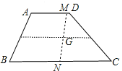
问题.试在图![]() 的梯形中画出至少五条黄金分割线,并说明理由.
的梯形中画出至少五条黄金分割线,并说明理由.
![]() 类似“黄金分割线”得“黄金分割面”定义:截面
类似“黄金分割线”得“黄金分割面”定义:截面![]() 将一个体积为
将一个体积为![]() 的图形分成体积为V1
的图形分成体积为V1
、![]() 的两个图形,且
的两个图形,且![]() ,则称直线
,则称直线![]() 为该图形的黄金分割面.
为该图形的黄金分割面.
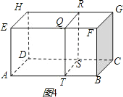
问题:如图![]() ,长方体
,长方体![]() 中,
中,![]() 是线段
是线段![]() 上的黄金分割点,证明经过
上的黄金分割点,证明经过![]() 点且平行于平面
点且平行于平面![]() 的截面
的截面![]() 是长方体的黄金分割面.
是长方体的黄金分割面.
【答案】(1)详见解析;(2)详见解析.
【解析】
(1)如图,先在梯形的中位线EF上找一个黄金分割点G,过点G作一条直线L交AD于点M,交BC于N,则MN就是梯形的黄金分割线.
(2)根据AT:AB=TB:AT,进而推出S矩形QRST=S矩形BCGF因为AT×S矩形QRST:AB×S矩形BCGF=TB×S矩形ADHE:AT×S矩形QRST从而不难求得截面QRST是长方体的黄金分割面.
解:![]() 如图,先在梯形的中位线
如图,先在梯形的中位线![]() 上找一个黄金分割点
上找一个黄金分割点![]() ,过点
,过点![]() 作一条直线
作一条直线![]() 交
交![]() 于点
于点![]() ,交
,交![]() 于
于![]() ,则
,则![]() 就是梯形的黄金分割线.
就是梯形的黄金分割线.
∵![]() ,
,
∴![]() ,
,
∵![]() ,
,![]() ,
,![]() (
(![]() 是梯形的高),
是梯形的高),
∴![]() ,
,
∵直线![]() 是过
是过![]() 的任意一条与
的任意一条与![]() ,
,![]() 都相交的直线,
都相交的直线,
∴符合题意的黄金分割线有无穷多条.
![]() ∵
∵![]() ,
,
∴![]() ,
,
∵![]() ,
,
即截面![]() 将体积为
将体积为![]() 的长方体,分成左右两块体积分别是
的长方体,分成左右两块体积分别是![]() ,
,![]() ,
,
∴![]() ,
,
∴截面![]() 是长方体的黄金分割面.
是长方体的黄金分割面.

练习册系列答案
 阳光课堂课时作业系列答案
阳光课堂课时作业系列答案
相关题目