Question

【题目】在平面直角坐标系xOy中，抛物线y=-x2+bx+c经过点A、B、C，已知A（-1，0），C（0，3）．

(1)求抛物线的表达式；

(2)如图1，P为线段BC上一点，过点P作y轴平行线，交抛物线于点D，当△BCD的面积最大时，求点P的坐标；

(3)如图2，抛物线顶点为E，EF⊥x轴于F点，N是线段EF上一动点，M（m，0）是x轴上一动点，若∠MNC=90°，直接写出实数m的取值范围．

Answer 1

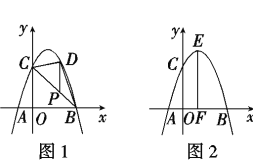
【答案】（1）y=-x2+2x+3；（2）P（，）；（3）

【解析】

（1）由y=-x2+bx+c经过点A、B、C，A（-1，0），C（0，3），利用待定系数法即可求得此抛物线的解析式；
（2）首先令-x2+2x+3=0，求得点B的坐标，然后设直线BC的解析式为y=kx+b′，由待定系数法即可求得直线BC的解析式，再设P（a，3-a），即可得D（a，-a2+2a+3），即可求得PD的长，由S△BDC=S△PDC+S△PDB，即可得S△BDC=，利用二次函数的性质，即可求得当△BDC的面积最大时，求点P的坐标；
（3）首先过C作CH⊥EF于H点，则CH=EH=1，然后分别从点M在EF左侧与M在EF右侧时去分析求解即可求得答案．

解：（1）由题，解得：，

所以抛物线表达式为

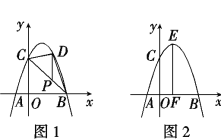
（2）令，

∴.即

设直线的表达式为，

∴

∴

故直线的表达式为，

设，则

当时，的面积最大，此时

（3）的取值范围是：