题目内容
如图12-1和12-2,△ABC中,∠BAC=90°,AB=AC,AD⊥BC,垂足是D,AE平分∠BAD,交BC于点E.过点A作AF⊥AE,过点C作CF∥AD,两直线交于点F.
( 1)在图12-1中,证明:△ACF≌△ABE;
1)在图12-1中,证明:△ACF≌△ABE;
 | |||
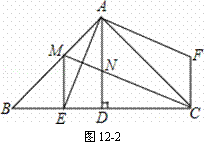 | |||
(2)在图12-2中,∠A CB的平分线交AB于点M,交AD于点N.
CB的平分线交AB于点M,交AD于点N.
① 求证:四边形ANCF是平行四边形;
② 求证:ME=MA;
③ 四边形ANCF是不是菱形?若是,请证明;若不是,请简要说明理由.
(1)证明:∵∠BAC=90°,AB=AC,
∴∠B=∠ACB=45°,
∵AD⊥BC
∴∠DAC=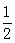 ∠CAB=45°
∠CAB=45°
∵CF∥AD
∴∠DAC=∠ACF=45°,
∴∠B=∠ACF=45°
∵AF⊥AE∴∠EAF=90°
∵∠EAF=∠EAC+∠CAF=90°
∠BAC=∠EAC+∠BAE=90°
∴∠CAF=∠BAE
∵AB=AC,
∴△ACF≌△ABE;
(2)①证明:∵∠BAC=90°, AB=AC,AD⊥BC
AB=AC,AD⊥BC
∴∠BAD=45°,
∵AE平分∠BAD,
∴∠BAE=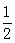 ∠DAB=22.5°,
∠DAB=22.5°,
∵△ACF≌△ABE;
∴∠BAE=∠CAF=22.5°,
∵∠ACB的平分线交AB于点M
∴∠ACM=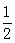 ∠ACB=22.5°,
∠ACB=22.5°,
∵∠ ACM =∠CAF=22.5°
∴AF∥CN
∵AD∥FC
∴四边形ANCF 是平行四边形;
是平行四边形;
②证明:∵∠BAC=90°,∠BAE=22.5°,
∴∠EAC=67.5°,
∵∠BCA=45°,
∴∠AEC=67.5°,
∵∠EAC=∠AEC=67.5°,
∴CA=CE
∵∠ACB的平分线交AB于点M
∴∠ACM=∠ECM
∵MC=MC
∴ △ACM≌△ECM
∴AM=EM
③答:不是.
理由:∵∠CAF=22.5°,∠ACF=45°
∴FA≠FC
∴四边形ANCF不是菱形

 ,点A是栏杆转动的支点,点E是栏杆两段的连接点,当车辆经过时,栏杆AEF升起后的位置如图1所示(图2为其几何图形)。其中AB⊥BC,DC⊥BC,EF∥BC,∠EAB=150°,AB=AE=1.2 m,BC=2.4m。
,点A是栏杆转动的支点,点E是栏杆两段的连接点,当车辆经过时,栏杆AEF升起后的位置如图1所示(图2为其几何图形)。其中AB⊥BC,DC⊥BC,EF∥BC,∠EAB=150°,AB=AE=1.2 m,BC=2.4m。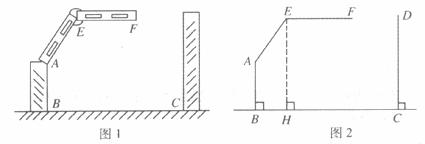
 ,结果精确到0.01 m,栏杆宽度忽略不计);
,结果精确到0.01 m,栏杆宽度忽略不计); C.40° D.50°
C.40° D.50°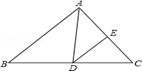
 B.8
B.8 D.12
D.12

 B.
B.
 D.
D.