题目内容
因式分解:
(1)9(3a+2b)2-25(a-2b)2
(2)
(3)
(4)(a2+ab+b2)2-9a2b2.
解:(1)9(3a+2b)2-25(a-2b)2,
=[3(3a+2b)+5(a-2b)][3(3a+2b)-5(a-2b)],
=(14a-4b)(4a+16b),
=8(7a-2b)(a+4b);
(2)(a-b)x2+(a-b)xy- (b-a)y2,
(b-a)y2,
=(a-b)(x2+xy+ y2),
y2),
=(a-b) ;
;
(3)a8-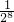 ,
,
=(a4)2-( ),
),
=(a4+ )(a4-
)(a4- ),
),
=(a4+ )(a2+
)(a2+ )(a2-
)(a2- ),
),
=(a4+ )(a2+
)(a2+ )(a+
)(a+ )(a-
)(a- );
);
(4)(a2+ab+b2)2-9a2b2
=(a2+ab+b2+3ab)(a2+ab+b2-3ab),
=(a2+4ab+b2)(a-b)2.
分析:(1)利用平方差公式分解因式,再进行整理即可;
(2)先提取公因式(a-b),再对余下的多项式利用完全平方公式分解因式;
(3)多次运用平方差公式分解因式即可;
(4)先按平方差公式,再按完全平方公式计算;
点评:本题考查了提公因式法与公式法分解因式,要求灵活使用各种方法对多项式进行因式分解,一般来说,如果可以先提取公因式的要先提取公因式,再考虑运用公式法分解.
=[3(3a+2b)+5(a-2b)][3(3a+2b)-5(a-2b)],
=(14a-4b)(4a+16b),
=8(7a-2b)(a+4b);
(2)(a-b)x2+(a-b)xy-
 (b-a)y2,
(b-a)y2,=(a-b)(x2+xy+
 y2),
y2),=(a-b)
 ;
;(3)a8-
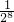 ,
,=(a4)2-(
 ),
),=(a4+
 )(a4-
)(a4- ),
),=(a4+
 )(a2+
)(a2+ )(a2-
)(a2- ),
),=(a4+
 )(a2+
)(a2+ )(a+
)(a+ )(a-
)(a- );
);(4)(a2+ab+b2)2-9a2b2
=(a2+ab+b2+3ab)(a2+ab+b2-3ab),
=(a2+4ab+b2)(a-b)2.
分析:(1)利用平方差公式分解因式,再进行整理即可;
(2)先提取公因式(a-b),再对余下的多项式利用完全平方公式分解因式;
(3)多次运用平方差公式分解因式即可;
(4)先按平方差公式,再按完全平方公式计算;
点评:本题考查了提公因式法与公式法分解因式,要求灵活使用各种方法对多项式进行因式分解,一般来说,如果可以先提取公因式的要先提取公因式,再考虑运用公式法分解.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目