Question

如图，已知在△ABC中，AB＜AC．
（1）用直尺和圆规在△ABC内部画∠CBD=∠C，BD与AC相交于点D；
（2）用直尺和圆规画△BCD的角平分线DE；
（3）作出△BCD中BD边上的高CF；
（4）度量BC与CE，发现CE=______BC．
（尺规作图，保留作图痕迹，不写作法）

Answer 1

解：（1）如图所示；

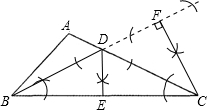
（2）如图所示；
（3）如图所示；
（4）BE=CE．
理由：∵∠CBD=∠C，
∴BD=CD，
∵DE平分∠BDC，
∴BE=CE（等腰三角形顶角的平分线，底边上的中线，底边上的高线互相重合）．
∴BE=BC．
分析：（1）根据作一个角等于已知角的作法作图；
（2）根据角平分线的作法作出△BDE的角平分线DE；
（3）延长BD，作⊥BD，即可得出答案；
（4）根据等腰三角形三线合一，顶角的平分线也是底边的中线．
点评：此题主要考查了角平分线的作法以及作一角等于已知角、等腰三角形的性质等知识，作钝角三角形中一锐角所对边上的高是考查重点．