题目内容
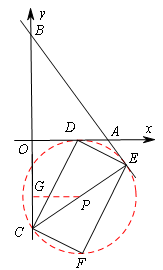
如图,在平面直角坐标系中,直线AB与x轴,y轴分别交于点A(6,0),B(0,8),点C的坐标为(0,m),过点C作CE⊥AB于点E,点D为x轴上一动点,连结CD,DE,以CD,DE为边作□CDEF。

(1)当0< m <8时,求CE的长(用含m的代数式表示);
(2)当m =3时,是否存在点D,使□CDEF的顶点F恰好落在y轴上?若存在,求出点D的坐标;若不存在,请说明理由;
(3)点D在整个运动过程中,若存在唯一的位置,使得□CDEF为矩形,请求出所有满足条件的m的值。

(1)当0< m <8时,求CE的长(用含m的代数式表示);
(2)当m =3时,是否存在点D,使□CDEF的顶点F恰好落在y轴上?若存在,求出点D的坐标;若不存在,请说明理由;
(3)点D在整个运动过程中,若存在唯一的位置,使得□CDEF为矩形,请求出所有满足条件的m的值。
(1)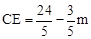 (2)存在(3)m的值为
(2)存在(3)m的值为 或0或
或0或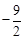 或
或
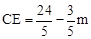 (2)存在(3)m的值为
(2)存在(3)m的值为 或0或
或0或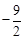 或
或
解:(1)∵A(6,0),B(0,8),∴OA=6,OB=8。∴AB=10。
∵∠CEB=∠EBC=900,∠OBA=∠EBC,∴△BCE∽△BAO。
∴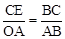 ,即
,即 。∴
。∴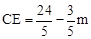 。
。
(2)存在。
∵m =3,∴BC=8-m=5, 。
。
∴根据勾股定理得BC=4。
∴AE=AB-BE=6。
∵点F落在y轴上(如图1),
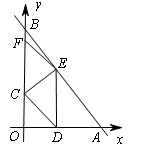
∴DE∥BO。
∴△EDA∽△BOA。∴ ,即
,即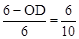 。
。
解得: 。∴点D的坐标为(
。∴点D的坐标为(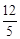 ,0)。
,0)。
(3)取CE的中点P,过点P作PG⊥y轴于点G,
则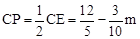 。
。
①当0< m <8时(如图2),
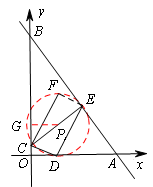
易证∠GCP=∠BAO,
∴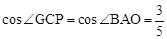 。
。
∴ 。
。
∴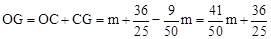 。
。
由题意,根据矩形对角线平分且相等的性质,得OG=CP,
∴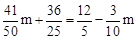 ,解得
,解得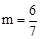 。
。
②当m≥8时,OG>CP,不存在满足条件的m的值。
③当m =0,即点C与点O重合时(如图3),
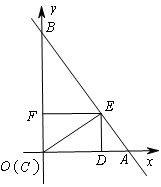
满足题意。
④当m<0时,分两种情况:
ⅰ)当点E与点A重合时(如图4),
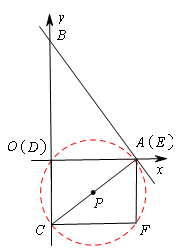
易证△COA∽△AOB,
∴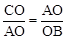 ,即
,即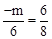 。
。
解得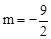 。
。
ⅱ)当点E与点A重合时(如图5),

 ,
,
由题意,得OG=CP,
∴ 。
。
解得 。
。
综上所述,m的值为 或0或
或0或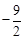 或
或 。
。
(1)由△BCE∽△BAO即可用含m的代数式表示出CE的长。
(2)由△EDA∽△BOA即可求得 ,从而得到点D的坐标。
,从而得到点D的坐标。
(3)分①0< m <8,②m≥8,③m =0,④m<0四种情况讨论。
∵∠CEB=∠EBC=900,∠OBA=∠EBC,∴△BCE∽△BAO。
∴
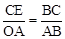 ,即
,即 。∴
。∴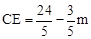 。
。(2)存在。
∵m =3,∴BC=8-m=5,
 。
。∴根据勾股定理得BC=4。
∴AE=AB-BE=6。
∵点F落在y轴上(如图1),

∴DE∥BO。
∴△EDA∽△BOA。∴
 ,即
,即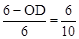 。
。解得:
 。∴点D的坐标为(
。∴点D的坐标为(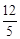 ,0)。
,0)。(3)取CE的中点P,过点P作PG⊥y轴于点G,
则
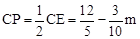 。
。①当0< m <8时(如图2),

易证∠GCP=∠BAO,
∴
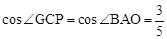 。
。∴
 。
。∴
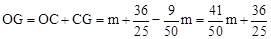 。
。由题意,根据矩形对角线平分且相等的性质,得OG=CP,
∴
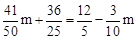 ,解得
,解得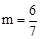 。
。②当m≥8时,OG>CP,不存在满足条件的m的值。
③当m =0,即点C与点O重合时(如图3),

满足题意。
④当m<0时,分两种情况:
ⅰ)当点E与点A重合时(如图4),

易证△COA∽△AOB,
∴
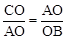 ,即
,即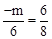 。
。解得
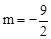 。
。ⅱ)当点E与点A重合时(如图5),


 ,
,由题意,得OG=CP,
∴
 。
。解得
 。
。综上所述,m的值为
 或0或
或0或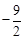 或
或 。
。(1)由△BCE∽△BAO即可用含m的代数式表示出CE的长。
(2)由△EDA∽△BOA即可求得
 ,从而得到点D的坐标。
,从而得到点D的坐标。(3)分①0< m <8,②m≥8,③m =0,④m<0四种情况讨论。

练习册系列答案
 新题型全程检测期末冲刺100分系列答案
新题型全程检测期末冲刺100分系列答案
相关题目
 的自变量x的取值范围是
的自变量x的取值范围是  自变量x的取值范围是【 】
自变量x的取值范围是【 】


 的自变量
的自变量 的取值范围是 。
的取值范围是 。