题目内容
已知a<b,用“>”或“<”填空.
(1)a+2______b+2
(2)a-4______b-4
(3)-5a______-5b
(4) ______
______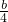
(5)-3a+1______-3b+1
(6)2a-2b______0
其中填“>”的题号是______,填“<”的题号是______.
解:(1)在不等式a<b的两边同时加上2,不等式仍成立,即a+2<b+2.
故填:<;
(2)在不等式a<b的两边同时减去2,不等式仍成立,即a-4<b-4.
故填:<;
(3)在不等式a<b的两边同时乘以-5,不等号的方向改变,即-5a>-5b.
故填:>;
(4)在不等式a<b的两边同时除以4,不等式仍成立,即 <
<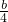 .
.
故填:<;
(5)在不等式a<b的两边同时乘以-3,不等号的方向改变,即-3a>-3b.
在不等式的两边同时加上1,不等式仍成立,即-3a+1>-3b+1;
故填:>;
(6)在不等式a的<b的两边同时乘以2,不等式仍成立,即2a<2b,
再在不等式的两边同时加上-2b,不等式仍成立,即2a-2b<0.
故填:<.
综上所述,填“>”的题号是 (3)、(5),填“<”的题号是 (1)、(2)、(4)、(6).
分析:根据不等式的性质进行填空.
点评:主要考查了不等式的基本性质:
(1)不等式两边加(或减)同一个数(或式子),不等号的方向不变.
(2)不等式两边乘(或除以)同一个正数,不等号的方向不变.
(3)不等式两边乘(或除以)同一个负数,不等号的方向改变.
故填:<;
(2)在不等式a<b的两边同时减去2,不等式仍成立,即a-4<b-4.
故填:<;
(3)在不等式a<b的两边同时乘以-5,不等号的方向改变,即-5a>-5b.
故填:>;
(4)在不等式a<b的两边同时除以4,不等式仍成立,即
 <
<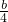 .
.故填:<;
(5)在不等式a<b的两边同时乘以-3,不等号的方向改变,即-3a>-3b.
在不等式的两边同时加上1,不等式仍成立,即-3a+1>-3b+1;
故填:>;
(6)在不等式a的<b的两边同时乘以2,不等式仍成立,即2a<2b,
再在不等式的两边同时加上-2b,不等式仍成立,即2a-2b<0.
故填:<.
综上所述,填“>”的题号是 (3)、(5),填“<”的题号是 (1)、(2)、(4)、(6).
分析:根据不等式的性质进行填空.
点评:主要考查了不等式的基本性质:
(1)不等式两边加(或减)同一个数(或式子),不等号的方向不变.
(2)不等式两边乘(或除以)同一个正数,不等号的方向不变.
(3)不等式两边乘(或除以)同一个负数,不等号的方向改变.

练习册系列答案
 亮点激活精编提优100分大试卷系列答案
亮点激活精编提优100分大试卷系列答案
相关题目

 20、如图,已知∠α,线段a,用直尺和圆规求作一个等腰三角形,使得底边为a,底角为∠α(只须作出正确图形,保留作图痕迹,不必写出作法).
20、如图,已知∠α,线段a,用直尺和圆规求作一个等腰三角形,使得底边为a,底角为∠α(只须作出正确图形,保留作图痕迹,不必写出作法). 如图,已知∠1=∠2,若用“SAS”判断△ACB≌△BDA,则还需补充的一个条件是
如图,已知∠1=∠2,若用“SAS”判断△ACB≌△BDA,则还需补充的一个条件是