��Ŀ����
����Ŀ���۲�̽����������⣮���ı���ABCD�У���E��F��G��H�ֱ��DZ�AB��BC��CD��DA���е㣬˳������E��F��G��H�õ����ı���EFGH�����е��ı��Σ�
��1����ͼ1����֤���е��ı���EFGH��ƽ���ı��Σ�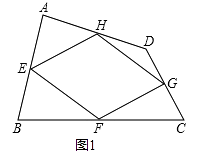
��2������̽������գ�
�ٵ��ı���ABCD���ƽ���ı���ʱ�������е��ı�������
�ڵ��ı���ABCD��ɾ���ʱ�������е��ı�������
�۵��ı���ABCD���������ʱ�������е��ı�������
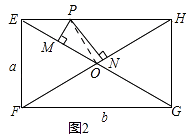
��3����ͼ2�����е��ı���EFGHΪ����ʱ���Խ���EG��FH�ཻ�ڵ�O��PΪEH�ϵĶ��㣬����P��PM��EG��PN��FH������ֱ�ΪM��N����EF=a��FG=b�����ж�PM+PN�ij��Ƿ�Ϊ��ֵ�����ǣ�����˶�ֵ�������ǣ�˵�����ɣ�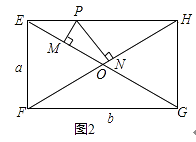
���𰸡�
��1��
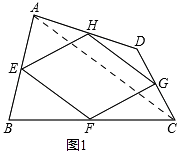
�⣺����AC����ͼ1��
�ڡ�DAC�У�HG��AC����HG= ![]() AC��
AC��
�ڡ�BAC�У�EF��AC����EF= ![]() AC��
AC��
��HG��EF����HG=EF��
���ı���EFGH��ƽ���ı���
��2��ƽ���ı��Σ����Σ�������
��3��
�⣺��ͼ��
����PO��
�ھ���EFGH�У�EO=HO= ![]() EG=
EG= ![]()
![]() ��
��
��S��EOH= ![]() S�ı���EFGH=
S�ı���EFGH= ![]() ab=S��POE+S��POH��
ab=S��POE+S��POH��
�� ![]() PM��EO+
PM��EO+ ![]() PN��HO=
PN��HO= ![]() ab��
ab��
�� ![]()
![]() ��PM+PN��=
��PM+PN��= ![]() ab��
ab��
��PM+PN= ![]() ��
��
��PM+PN�Ƕ�ֵ
���������⣺ ��2�����ڡ�DAC�У�HG��AC����HG= ![]() AC��
AC��
�ڡ�BAC�У�EF��AC����EF= ![]() AC��
AC��
��HG��EF����HG=EF��
���ı���EFGH��ƽ���ı��Σ�
���Դ���ƽ���ı��Σ�
���ɣ�1���У��ı���EFGH��ƽ���ı��Σ�
ͬ��1���ķ����ã�EH= ![]() BD��
BD��
���ı���ABCD�Ǿ��Σ�
��AC=BD
��EH=EF��
��ƽ���ı���ABCD�����Σ�
���Դ������Σ�
���ɣ�2�����У��ı���EFGH�����Σ�
���ı���ABCD�������Σ�
��AC��BD��
���EFG=90�㣬
������ABCD��������
���Դ��������Σ�