Question

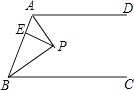
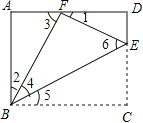
【题目】（本题9分）如图，点E是矩形ABCD中CD边上一点，△BCE沿BE折叠为△BFE,点F落在AD上.

(1)求证：△ABF∽△DFE

(2)若△BEF也与△ABF相似，请求出的值 .

Answer 1

【答案】（1）证明见解析；（2）.

【解析】试题分析：（1）在△ABF与△DFE中的对应角∠A=∠D=90°，∠2=∠1，易证△ABF∽△DFE；

（2）需要分类讨论：①△ABF∽△FBE；②△ABF∽△FEB时求出的值．

试题解析：（1）∵四边形ABCD是矩形，∴∠A=∠D=∠C=90°.

∵△BCE沿BE折叠为△BFE，∴∠BFE=∠C="90°." ∴∠AFB+∠DFE=180°﹣∠BFE=90°.

又∠AFB+∠ABF=90°，∴∠ABF=∠DFE。∴△ABE∽△DFE.

（2）①当△ABF∽△FBE时，∠2=∠4．

∵∠4=∠5，∠2+∠4+∠5=90°，∴∠2=∠4=∠5=30°.

∴设CE=EF=x，则BC=x，DE=x. ∴DC=x. ∴.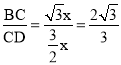

②当△ABF∽△FEB时，∠2=∠6，

∵∠4+∠6=90°，∴∠2+∠4=90°，这与∠2+∠4+∠5=90°相矛盾. ∴△ABF∽△FEB不成立．

综上所述， 的值是.