题目内容
△ABC中,AB=AC,AD是底边BC上的高,DE⊥AC于E,G是DE的中点,AG,BE相交于点H,BE,AD相交于点M
(1)如图a,若∠BAC=60°,求证:△ADG∽△BCE;
(2)如图b,连接DH,AM=1,BE=4AG,求DH的长.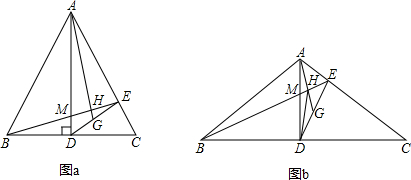
(1)证明:∵∠BAC=60°,AB=AC,AD⊥BC,DE⊥AC,
∴BD=DC,∠DAC=∠EDC=30°,
∴在Rt△DEC中,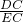 =2,
=2,
∴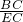 =4,
=4,
在Rt△ADE中,
∵ =2,
=2,
∴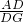 =4,
=4,
∴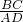 =
=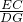 ,
,
∵∠ADE=∠C,
∴△ADG∽△BCE;
(2)解:∵∠ADE+∠EDC=90°,
∴∠ADE=∠C,
∵∠DEC=∠AED=90°,
∴△CDE∽△DAE,
∴ =
=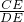 ,
,
∴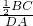 =
= ,
,
∴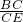 =
=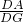 ,∠ADE=∠C,
,∠ADE=∠C,
∴△ADG∽△BCE,
∴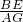 =
=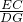 =4,
=4,
∴ =
= =2,
=2,
∴tanC= ,
,
∴∠DAG=∠EBC,∠AMH=∠BMD,
∴∠AHE=∠ADB=90°,
设DG= a,则GE=
a,则GE= a,EC=4
a,EC=4 a,DC=10a,
a,DC=10a,
∴AD=5a,AE= a,
a,
∴∠AGE=45°,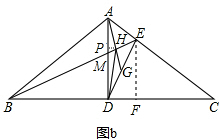
过点E作EF⊥BC于点F,过点H作GP⊥AD于点P,
∴EF=4a,FC=8a,BF=12a,
∵MD∥EF,
∴△BMD∽△BEF,
∴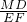 =
=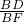 ,
,
∴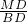 =
= =
=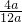 =
= =tan∠MBD=tan∠DAG=
=tan∠MBD=tan∠DAG= ,
,
在Rt△AHE中,AH=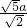 =
= a,
a,
在Rt△AMH中,
∵AM= a=1,
a=1,
∴a= ,AD=3,
,AD=3,
∴AH= ,AP=
,AP= ,DP=
,DP= ,PH=
,PH= ,
,
∴DH=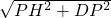 =
= .
.
分析:(1)先根据∠BAC=60°,AB=AC,AD⊥BC,DE⊥AC,可得出BD=DC,∠DAC=∠EDC=30°,在Rt△DEC中,由直角三角形的性质可知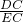 =2,所以
=2,所以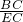 =4,同理可得在Rt△ADE中,
=4,同理可得在Rt△ADE中, =2,
=2,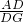 =4,
=4,
故可得出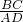 =
=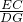 ,再由∠ADE=∠C即可得出结论;
,再由∠ADE=∠C即可得出结论;
(2)由∠ADE+∠EDC=90°可知∠ADE=∠C,由相似三角形的判定定理可知△CDE∽△DAE,故可得出 =
=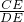 ,即
,即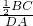 =
= ,
,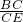 =
=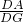 ,∠ADE=∠C,进而得出△ADG∽△BCE,tanC=
,∠ADE=∠C,进而得出△ADG∽△BCE,tanC= ,故可得出∠AHE=∠ADB=90°,设DG=
,故可得出∠AHE=∠ADB=90°,设DG= a,则GE=
a,则GE= a,EC=4
a,EC=4 a,DC=10a,所以AD=5a,AE=
a,DC=10a,所以AD=5a,AE= a,∠AGE=45°,过点E作EF⊥BC于点F,过点H作GP⊥AD于点P,根据MD∥EF可知△BMD∽△BEF,所以
a,∠AGE=45°,过点E作EF⊥BC于点F,过点H作GP⊥AD于点P,根据MD∥EF可知△BMD∽△BEF,所以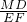 =
=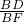 ,
,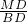 =
= =
=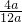 =
= =tan∠MBD=tan∠DAG=
=tan∠MBD=tan∠DAG= ,在Rt△AHE中可用a表示出AH的长,在Rt△AMH中,根据AM=
,在Rt△AHE中可用a表示出AH的长,在Rt△AMH中,根据AM= a=1求出a的值,故可得出AH,AP,DP,PH的长,根据勾股定理即可得出结论.
a=1求出a的值,故可得出AH,AP,DP,PH的长,根据勾股定理即可得出结论.
点评:本题考查的是相似三角形的判定与性质,根据题意作出辅助线,构造出相似三角形,利用相似三角形的性质求解是解答此题的关键.
∴BD=DC,∠DAC=∠EDC=30°,
∴在Rt△DEC中,
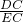 =2,
=2,∴
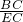 =4,
=4,在Rt△ADE中,
∵
 =2,
=2,∴
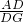 =4,
=4,∴
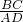 =
=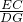 ,
,∵∠ADE=∠C,
∴△ADG∽△BCE;
(2)解:∵∠ADE+∠EDC=90°,
∴∠ADE=∠C,
∵∠DEC=∠AED=90°,
∴△CDE∽△DAE,
∴
 =
=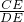 ,
,∴
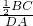 =
= ,
,∴
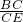 =
=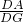 ,∠ADE=∠C,
,∠ADE=∠C,∴△ADG∽△BCE,
∴
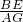 =
=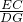 =4,
=4,∴
 =
= =2,
=2,∴tanC=
 ,
,∴∠DAG=∠EBC,∠AMH=∠BMD,
∴∠AHE=∠ADB=90°,
设DG=
 a,则GE=
a,则GE= a,EC=4
a,EC=4 a,DC=10a,
a,DC=10a,∴AD=5a,AE=
 a,
a,∴∠AGE=45°,

过点E作EF⊥BC于点F,过点H作GP⊥AD于点P,
∴EF=4a,FC=8a,BF=12a,
∵MD∥EF,
∴△BMD∽△BEF,
∴
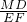 =
=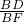 ,
,∴
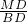 =
= =
=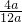 =
= =tan∠MBD=tan∠DAG=
=tan∠MBD=tan∠DAG= ,
,在Rt△AHE中,AH=
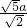 =
= a,
a,在Rt△AMH中,
∵AM=
 a=1,
a=1,∴a=
 ,AD=3,
,AD=3,∴AH=
 ,AP=
,AP= ,DP=
,DP= ,PH=
,PH= ,
,∴DH=
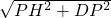 =
= .
.分析:(1)先根据∠BAC=60°,AB=AC,AD⊥BC,DE⊥AC,可得出BD=DC,∠DAC=∠EDC=30°,在Rt△DEC中,由直角三角形的性质可知
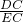 =2,所以
=2,所以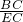 =4,同理可得在Rt△ADE中,
=4,同理可得在Rt△ADE中, =2,
=2,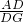 =4,
=4,故可得出
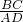 =
=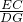 ,再由∠ADE=∠C即可得出结论;
,再由∠ADE=∠C即可得出结论;(2)由∠ADE+∠EDC=90°可知∠ADE=∠C,由相似三角形的判定定理可知△CDE∽△DAE,故可得出
 =
=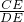 ,即
,即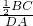 =
= ,
,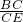 =
=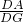 ,∠ADE=∠C,进而得出△ADG∽△BCE,tanC=
,∠ADE=∠C,进而得出△ADG∽△BCE,tanC= ,故可得出∠AHE=∠ADB=90°,设DG=
,故可得出∠AHE=∠ADB=90°,设DG= a,则GE=
a,则GE= a,EC=4
a,EC=4 a,DC=10a,所以AD=5a,AE=
a,DC=10a,所以AD=5a,AE= a,∠AGE=45°,过点E作EF⊥BC于点F,过点H作GP⊥AD于点P,根据MD∥EF可知△BMD∽△BEF,所以
a,∠AGE=45°,过点E作EF⊥BC于点F,过点H作GP⊥AD于点P,根据MD∥EF可知△BMD∽△BEF,所以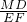 =
=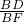 ,
,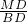 =
= =
=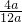 =
= =tan∠MBD=tan∠DAG=
=tan∠MBD=tan∠DAG= ,在Rt△AHE中可用a表示出AH的长,在Rt△AMH中,根据AM=
,在Rt△AHE中可用a表示出AH的长,在Rt△AMH中,根据AM= a=1求出a的值,故可得出AH,AP,DP,PH的长,根据勾股定理即可得出结论.
a=1求出a的值,故可得出AH,AP,DP,PH的长,根据勾股定理即可得出结论.点评:本题考查的是相似三角形的判定与性质,根据题意作出辅助线,构造出相似三角形,利用相似三角形的性质求解是解答此题的关键.

练习册系列答案
 发散思维新课堂系列答案
发散思维新课堂系列答案
相关题目
 如图,在△ABC中,AB=AC,∠A=36°,
如图,在△ABC中,AB=AC,∠A=36°, 15、如图,在△ABC中,AB=AC,点D,E在直线BC上运动.如果∠DAE=l05°,△ABD∽△ECA,则∠BAC=
15、如图,在△ABC中,AB=AC,点D,E在直线BC上运动.如果∠DAE=l05°,△ABD∽△ECA,则∠BAC= △ABC中,AB=AC,D、E分别是AB、AC的中点,若AB=4,BC=6,则△ADE的周长是
△ABC中,AB=AC,D、E分别是AB、AC的中点,若AB=4,BC=6,则△ADE的周长是 ,连接AO、BE、DC.
,连接AO、BE、DC.