题目内容
如图所示,分别在三角形,四边形,五边形的广场各角修建半径为1米的扇形草坪(图中阴影部分).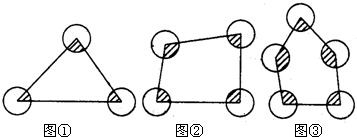
(1)图①中草坪的面积为
(2)图②中草坪的面积为
(3)图③中草坪的面积为
(4)如果多边形的边数为n,其余条件不变,那么,你认为草坪的面积为多少?(写出过程)
分析:依题意,因为半径为1的圆面积为π.图1的草坪形成的内角和度数为180°,为一个半圆,所以草坪的面积为
π;以此类推,易求出草坪的面积.
| 1 |
| 2 |
解答:解:(1)因为半径为1的圆面积为π,故该草坪形成的内角和度数为(3-2)×180°=180°,所以草坪的面积为
π.
(2)图2草坪形成四边形,故(4-2)×180°=360°,为一个圆,故草坪的面积为π.
(3)图3草坪形成一个五边形,故(5-2)×180°=540°,故草坪的面积为
π.
(4)根据以上的规律可知,当多边形的边数为n,所以草坪的面积为
πR2.
| 1 |
| 2 |
(2)图2草坪形成四边形,故(4-2)×180°=360°,为一个圆,故草坪的面积为π.
(3)图3草坪形成一个五边形,故(5-2)×180°=540°,故草坪的面积为
| 3 |
| 2 |
(4)根据以上的规律可知,当多边形的边数为n,所以草坪的面积为
| n-2 |
| 2 |
点评:本题难度属中等.主要考查多边形内角与圆相结合的知识.

练习册系列答案
 学而优暑期衔接南京大学出版社系列答案
学而优暑期衔接南京大学出版社系列答案 Happy holiday欢乐假期暑假作业广东人民出版社系列答案
Happy holiday欢乐假期暑假作业广东人民出版社系列答案
相关题目




