Question

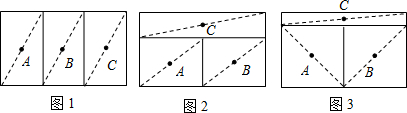
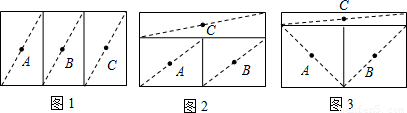
三个牧童A、B、C在一块正方形的牧场上看守一群牛，为保证公平合理，他们商量将牧场划分为三块分别看守，划分的原则是：①每个人看守的牧场面积相等；②在每个区域内，各选定一个看守点，并保证在有情况时他们所需走的最大距离（看守点到本区域内最远处的距离）相等．按照这一原则，他们先设计了一种如图1的划分方案：把正方形牧场分成三块相等的矩形，大家分头守在这三个矩形的中心（对角线交点），看守自己的一块牧场．

过了一段时间，牧童B和牧童C又分别提出了新的划分方案．

牧童B的划分方案如图2：三块矩形的面积相等，牧童的位置在三个小矩形的中心．

牧童C的划分方案如图3：把正方形的牧场分成三块矩形，牧童的位置在三个小矩形的中心，并保证在有情况时三个人所需走的最大距离相等．

请回答：

（1）牧童B的划分方案中，牧童      （填A、B或C）在有情况时所需走的最大距离较远；

（2）牧童C的划分方案是否符合他们商量的划分原则？为什么？（提示：在计算时可取正方形边长为2）

Answer 1

（1） C  ；

  （2）牧童C的划分方案不符合他们商量的划分原则．     

理由如下

：如图，在正方形DEFG中，四边形HENM、MNFP、DHPG都是矩形，且HN=NP=HG．可知EN=NF，S_矩形HENM＝ S_矩形MNFP．   

取正方形边长为2，设HD=x，则HE=2－x.

在Rt△HEN和Rt△DHG中，

由HN=HG得：EH²+EN²=DH²+DG² ，

即：．

解得，．∴． 

        ∴S_矩形HENM = S_矩形MNFP =，S_矩形DHPG =．∴S_矩形HENM ≠ S_矩形DHPG．

∴牧童C的划分方案不符合他们商量的划分原则．