题目内容
 如图,已知等边三角形ABC周长为1,△ABC的三条中位线组成△A1B1C1,△A1B1C1的三条中位线组成的△A2B2C2,依此进行下去得△A5B5C5的周长为
如图,已知等边三角形ABC周长为1,△ABC的三条中位线组成△A1B1C1,△A1B1C1的三条中位线组成的△A2B2C2,依此进行下去得△A5B5C5的周长为| 1 |
| 25 |
| 1 |
| 25 |
| 1 |
| 2n |
| 1 |
| 2n |
分析:根据三角形的中位线平行于第三边并且等于第三边的一半求出A1B1=AC,B1C1=AB,A1C1=BC,从而得到△A1B1C1是△ABC周长的一半,依此类推,下一个三角形是上一个三角形的周长的一半,根据此规律求解即可.
解答:解:∵△ABC的三条中位线组成△A1B1C1,
∴A1B1=AC,B1C1=AB,A1C1=BC,
∴△A1B1C1的周长=
△ABC的周长=
,
依此类推,△A2B2C2的周长=
△A1B1C1的周长=
×
=
,
…,
∴△A5B5C5的周长=
,
△AnBnCn的周长=
.
故答案为:
;
.
∴A1B1=AC,B1C1=AB,A1C1=BC,
∴△A1B1C1的周长=
| 1 |
| 2 |
| 1 |
| 2 |
依此类推,△A2B2C2的周长=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 22 |
…,
∴△A5B5C5的周长=
| 1 |
| 25 |
△AnBnCn的周长=
| 1 |
| 2n |
故答案为:
| 1 |
| 25 |
| 1 |
| 2n |
点评:本题考查了三角形的中位线平行于第三边并且等于第三边的一半的性质,求出后一个三角形的周长等于前一个三角形的周长的一半是解题的关键.

练习册系列答案
 优加精卷系列答案
优加精卷系列答案
相关题目
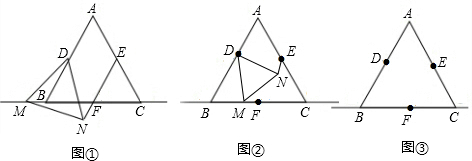
 23、如图,已知等边三角形ABC,在AB上取点D,在AC上取点E,使得AD=AE,作等边三角形PCD,QAE和RAB,求证:P、Q、R是等边三角形的三个顶点.
23、如图,已知等边三角形ABC,在AB上取点D,在AC上取点E,使得AD=AE,作等边三角形PCD,QAE和RAB,求证:P、Q、R是等边三角形的三个顶点.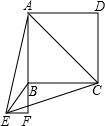 如图,已知等边三角形△AEC,以AC为对角线做正方形ABCD(点B在△AEC内,点D在△AEC外).连接EB,过E作EF⊥AB,交AB的延长线为F.
如图,已知等边三角形△AEC,以AC为对角线做正方形ABCD(点B在△AEC内,点D在△AEC外).连接EB,过E作EF⊥AB,交AB的延长线为F. 如图,已知等边三角形△AEC,以AC为对角线做正方形ABCD(点B在△AEC内,点D在△AEC外).连接EB,过E作EF⊥AB,交AB的延长线为F.请猜测直线BE和直线AC的位置关系,并证明你的猜想.
如图,已知等边三角形△AEC,以AC为对角线做正方形ABCD(点B在△AEC内,点D在△AEC外).连接EB,过E作EF⊥AB,交AB的延长线为F.请猜测直线BE和直线AC的位置关系,并证明你的猜想. 如图,已知等边三角形ABC的边长为10,点P、Q分别为边AB、AC上的一个动点,点P从点B出发以1cm/s的速度向点A运动,点Q从点C出发以2cm/s的速度向点A运动,连接PQ,以Q为旋转中心,将线段PQ按逆时针方向旋转60°得线段QD,若点P、Q同时出发,则当运动
如图,已知等边三角形ABC的边长为10,点P、Q分别为边AB、AC上的一个动点,点P从点B出发以1cm/s的速度向点A运动,点Q从点C出发以2cm/s的速度向点A运动,连接PQ,以Q为旋转中心,将线段PQ按逆时针方向旋转60°得线段QD,若点P、Q同时出发,则当运动