题目内容
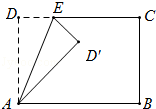
【题目】如图,菱形ABCD的对角线AC、BD相交于点O,过点D作DE∥AC,且DE= ![]() AC,连接CE、OE,连接AE交OD于点F.
AC,连接CE、OE,连接AE交OD于点F. 
(1)求证:OE=CD;
(2)若菱形ABCD的边长为4,∠ABC=60°,求AE的长.
【答案】
(1)证明:在菱形ABCD中,OC= ![]() AC.
AC.
∴DE=OC.
∵DE∥AC,
∴四边形OCED是平行四边形.
∵AC⊥BD,
∴平行四边形OCED是矩形.
∴OE=CD
(2)解:在菱形ABCD中,∠ABC=60°,
∴AC=AB=4.
∴在矩形OCED中,CE=OD= ![]() =2
=2 ![]() .
.
在Rt△ACE中,
AE= ![]() =2
=2 ![]()
【解析】(1)先求出四边形OCED是平行四边形,再根据菱形的对角线互相垂直求出∠COD=90°,证明OCED是矩形,可得OE=CD即可;(2)根据菱形的性质得出AC=AB,再根据勾股定理得出AE的长度即可.
【考点精析】解答此题的关键在于理解菱形的性质的相关知识,掌握菱形的四条边都相等;菱形的对角线互相垂直,并且每一条对角线平分一组对角;菱形被两条对角线分成四个全等的直角三角形;菱形的面积等于两条对角线长的积的一半.

练习册系列答案
相关题目
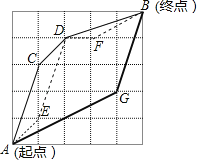
【题目】嘉嘉参加机器人设计活动,需操控机器人在5×5的方格棋盘上从A点行走至B点,且每个小方格皆为正方形,主办单位规定了三条行走路径R1,R2,R3,其行经位置如图与表所示:
路径 | 编号 | 图例 | 行径位置 |
第一条路径 | R1 | _ | A→C→D→B |
第二条路径 | R2 | … | A→E→D→F→B |
第三条路径 | R3 | ▂ | A→G→B |
已知A、B、C、D、E、F、G七点皆落在格线的交点上,且两点之间的路径皆为直线,在无法使用任何工具测量的条件下,请判断R1、R2、R3这三条路径中,最长与最短的路径分别为何?请写出你的答案,并完整说明理由.