题目内容
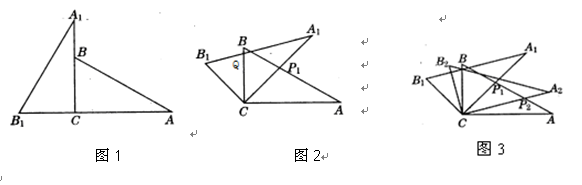
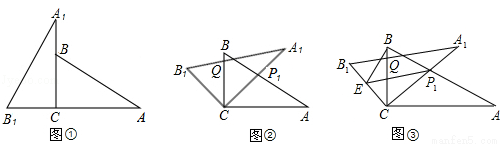
将两块全等的三角板如图1摆放,其中∠A1CB1=∠ACB=90°,∠A1=∠A=30°。【小题1】(1)将图1中△A1B1C绕点C顺时针旋转45°得图2,点
 与AB的交点,点Q是
与AB的交点,点Q是 与BC的交点,求证:
与BC的交点,求证: =
= ;
;【小题2】(2)在图2中,若AP1=
 ,则CQ等于多少?
,则CQ等于多少?【小题3】(3)将图2中△
 绕点C顺时针旋转到△
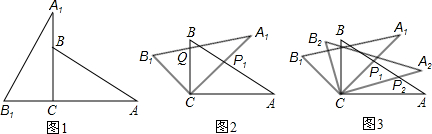
绕点C顺时针旋转到△ (如图3),点
(如图3),点 与AP1的交点.当旋转角为多少度时,有△A P1C∽△CP1P2? 这时线段
与AP1的交点.当旋转角为多少度时,有△A P1C∽△CP1P2? 这时线段 之间存在一个怎样的数量关系?.
之间存在一个怎样的数量关系?.
【小题1】⑴证明:∵∠B1CB=45°,∠B1CA1=90°,∴∠B1CQ=∠BCP1=45°;
又B1C=BC,∠B1=∠B,∴△B1CQ≌△BCP1(ASA)∴CQ=CP1
【小题2】⑵解:作P1D⊥AC于D,∵∠A=30°∴P1D=
 AP1;
AP1;∵∠P1CD=45°,∴
 =sin45°=
=sin45°= ,∴CP1=
,∴CP1= P1D=
P1D= AP1;
AP1;又AP1=
 ,CQ=CP1 ,∴CQ=
,CQ=CP1 ,∴CQ=

【小题3】⑶解:当∠P1CP2=∠P1AC=30°时,由于∠CP1P2=∠AP1C,
则△AP1C∽△CP1P2, 这时
 ,
,∴P1P2=
 CP1 . 解析:
CP1 . 解析:略

练习册系列答案
相关题目


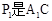 与AB的交点,点Q是
与AB的交点,点Q是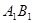 与BC的交点,求证:
与BC的交点,求证: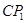 =
=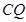 ;
; ,则CQ等于多少?
,则CQ等于多少?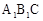 绕点C顺时针旋转到△
绕点C顺时针旋转到△ (如图3),点
(如图3),点 与AP1的交点.当旋转角为多少度时,有△A P1C∽△CP1P2? 这时线段
与AP1的交点.当旋转角为多少度时,有△A P1C∽△CP1P2? 这时线段 之间存在一个怎样的数量关系?.
之间存在一个怎样的数量关系?.