题目内容
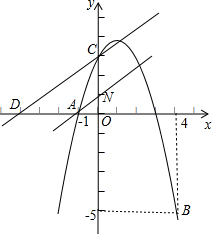 如图,已知抛物线经过点A(-1,0),B(4,-5),C (0,3).
如图,已知抛物线经过点A(-1,0),B(4,-5),C (0,3).(1)求抛物线的解析式;
(2)若直线CD的解析式为y=x+b,将直线CD沿着y轴方向平移2个单位得直线AN,交x、y轴于点A、N.
①求直线AN的解析式;
②在抛物线的对称轴上是否存在点P,使得以点P为圆心的圆同时与直线AN、y轴相切?若有,求出点P的坐标.
分析:(1)利用待定系数法求二次函数解析式即可得出答案;
(2)根据将点C(0,3)代入y=x+b,即可得出一次函数解析式;
(3)根据y=-x2+2x+3的对称轴是X=1,得出直线y=x+1与对称轴X=1的交点坐标是(1,2),再利用等腰直角三角形的性质求出.
(2)根据将点C(0,3)代入y=x+b,即可得出一次函数解析式;
(3)根据y=-x2+2x+3的对称轴是X=1,得出直线y=x+1与对称轴X=1的交点坐标是(1,2),再利用等腰直角三角形的性质求出.
解答:解:(1)∵抛物线经过点A(-1,0),B(4,-5),
C (0,3).
∴
,
解得:
,
∴抛物线的解析式是y=-x2+2x+3;

(2)将点C(0,3)代入y=x+b,
解得b=3,
所以直线AN的解析式y=x+1;
(3)y=-x2+2x+3的对称轴是x=1,
直线y=x+1与对称轴X=1的交点坐标是(1,2),依题意设p(1,y).
当点p在直线y=x+1的下方(如图2),
证明△MFP是等腰直角三角形后可得EP=FP=FM=1,
所以MP=
,所以
+y=2,即y=2-
,所以P点的坐标是(1,2-
).
当点p在直线y=x+1的上方(如图3),
证明△MFP是等腰直角三角形后可得EP=FP=FM=1,
所以MP=
,所以y=2+
,所以P点的坐标是(1,2+
).
C (0,3).
∴
|
解得:
|
∴抛物线的解析式是y=-x2+2x+3;

(2)将点C(0,3)代入y=x+b,
解得b=3,
所以直线AN的解析式y=x+1;
(3)y=-x2+2x+3的对称轴是x=1,
直线y=x+1与对称轴X=1的交点坐标是(1,2),依题意设p(1,y).
当点p在直线y=x+1的下方(如图2),
证明△MFP是等腰直角三角形后可得EP=FP=FM=1,
所以MP=
| 2 |
| 2 |
| 2 |
| 2 |
当点p在直线y=x+1的上方(如图3),
证明△MFP是等腰直角三角形后可得EP=FP=FM=1,
所以MP=
| 2 |
| 2 |
| 2 |
点评:此题主要考查了待定系数法求二次函数解析式以及求一次函数解析式和等腰直角三角形的性质等知识,利用数形结合进行分类讨论是这部分考查重点同学们应重点掌握.

练习册系列答案
 学而优衔接教材南京大学出版社系列答案
学而优衔接教材南京大学出版社系列答案 小学课堂作业系列答案
小学课堂作业系列答案 金博士一点全通系列答案
金博士一点全通系列答案
相关题目
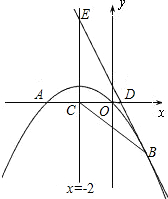 2x+1经过抛物线上一点B(2,m),且与y轴.直线x=-2分别交于点D、E.
2x+1经过抛物线上一点B(2,m),且与y轴.直线x=-2分别交于点D、E. (2013•衡阳)如图,已知抛物线经过A(1,0),B(0,3)两点,对称轴是x=-1.
(2013•衡阳)如图,已知抛物线经过A(1,0),B(0,3)两点,对称轴是x=-1. 如图,已知抛物线经过原点O和x轴上另一点A,它的对称轴x=2与x轴交于点C,直线y=-2x-1经过抛物线上一点B(-2,m),且与y轴、直线x=2分别交于点D、E,
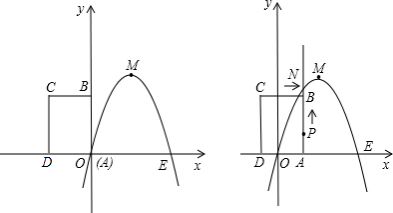
如图,已知抛物线经过原点O和x轴上另一点A,它的对称轴x=2与x轴交于点C,直线y=-2x-1经过抛物线上一点B(-2,m),且与y轴、直线x=2分别交于点D、E, 如图,已知抛物线经过坐标原点,与x轴的另一个交点为A,且顶点M坐标为(1,2),
如图,已知抛物线经过坐标原点,与x轴的另一个交点为A,且顶点M坐标为(1,2),