题目内容
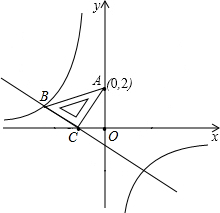 (2013•平遥县模拟)如图,在平面直角坐标系中,将一块等腰直角三角板ABC放在第二象限,斜靠在两坐标轴上,点C坐标为(-1,0),tan∠ACO=2.一次函数y=kx+b的图象经过点B、C,反比例函数y=
(2013•平遥县模拟)如图,在平面直角坐标系中,将一块等腰直角三角板ABC放在第二象限,斜靠在两坐标轴上,点C坐标为(-1,0),tan∠ACO=2.一次函数y=kx+b的图象经过点B、C,反比例函数y=| m |
| x |
(1)求一次函数和反比例函数的关系式;
(2)直接写出当x<0时,kx+b-
| m |
| x |
(3)在x轴上找一点M,使得AM+BM的值最小,并求出点M的坐标和AM+BM的最小值.
分析:(1)在Rt△AOC中求出AC的长度,然后求出sin∠CAO的值,过点B作BF⊥x轴于点F,由∠BCF=∠CAO,可求出BF,继而得出FC,从而求得点B的坐标,利用待定系数法可求出一次函数和反比例函数的关系式;
(2)不等式的含义为:当x<0时,求出一次函数值y=kx+b小于反比例函数y=
的x的取值范围,结合图形即可直接写出答案.
(3)根据轴对称的性质,找到点A关于x的对称点A',连接BA',则BA'与x轴的交点即为点M的位置,求出直线BA'的解析式,可得出点M的坐标,根据B、A'的坐标可求出AM+BM的最小值.
(2)不等式的含义为:当x<0时,求出一次函数值y=kx+b小于反比例函数y=
| m |
| x |
(3)根据轴对称的性质,找到点A关于x的对称点A',连接BA',则BA'与x轴的交点即为点M的位置,求出直线BA'的解析式,可得出点M的坐标,根据B、A'的坐标可求出AM+BM的最小值.
解答:解:(1)过点B作BF⊥x轴于点F,

在Rt△AOC中,AC=
=
,则sin∠CAO=
=
,
∵∠BCA=90°,
∴∠BCF+∠ACO=90°,
又∵∠CAO+∠ACO=90°,
∴∠BCF=∠CAO,
∴sin∠BCF=sin∠CAO=
=
,
∴BF=1,
∴CF=
=2,
∴点B的坐标为(-3,1),
将点B的坐标代入反比例函数解析式可得:1=
,
解得:k=-3,
故可得反比例函数解析式为y=-
;
将点B、C的坐标代入一次函数解析式可得:
,
解得:
.
故可得一次函数解析式为y=-
x-
.
(2)结合点B的坐标及图象,可得当x<0时,kx+b-
<0的解集为:-3<x<0;
(3)作点A关于x轴的对称点A′,连接 B A′与x轴 的交点即为点M,

设直线BA'的解析式为y=ax+b,将点A'及点B的坐标代入可得:
,
解得:
.
故直线BA'的解析式为y=-x-2,
令y=0,可得-x-2=0,
解得:x=-2,
故点M 的坐标为(-2,0),
AM+BM=BM+MA′=BA′=
=3
.
综上可得:点M的坐标为(-2,0),AM+BM的最小值为3
.

在Rt△AOC中,AC=
| OA2+OC2 |
| 5 |
| OC |
| AC |
| ||
| 5 |
∵∠BCA=90°,
∴∠BCF+∠ACO=90°,
又∵∠CAO+∠ACO=90°,
∴∠BCF=∠CAO,
∴sin∠BCF=sin∠CAO=
| BF |
| BC |
| ||
| 5 |
∴BF=1,
∴CF=
| BC2-BF2 |
∴点B的坐标为(-3,1),
将点B的坐标代入反比例函数解析式可得:1=
| k |
| -3 |
解得:k=-3,
故可得反比例函数解析式为y=-
| 3 |
| x |
将点B、C的坐标代入一次函数解析式可得:
|
解得:
|
故可得一次函数解析式为y=-
| 1 |
| 2 |
| 1 |
| 2 |
(2)结合点B的坐标及图象,可得当x<0时,kx+b-
| m |
| x |
(3)作点A关于x轴的对称点A′,连接 B A′与x轴 的交点即为点M,

设直线BA'的解析式为y=ax+b,将点A'及点B的坐标代入可得:
|
解得:
|
故直线BA'的解析式为y=-x-2,
令y=0,可得-x-2=0,
解得:x=-2,
故点M 的坐标为(-2,0),
AM+BM=BM+MA′=BA′=
| (-3-0)2+[1-(-2)]2 |
| 2 |
综上可得:点M的坐标为(-2,0),AM+BM的最小值为3
| 2 |
点评:本题考查了反比例函数的综合应用,涉及了待定系数法求函数解析式、轴对称求最短路径及一次函数与反比例函数的交点问题,综合考察的知识点较多,注意培养自己解综合题的能力,将所学知识融会贯通.

练习册系列答案
 期末金牌卷系列答案
期末金牌卷系列答案 轻松课堂标准练系列答案
轻松课堂标准练系列答案
相关题目
 (2013•平遥县模拟)如图,AB∥CD,∠BAC=120°,则∠C的度数是( )
(2013•平遥县模拟)如图,AB∥CD,∠BAC=120°,则∠C的度数是( ) (2013•平遥县模拟)如图是二次函数y=ax2+bx+c的图象,在下列说法中:①abc>0;②a+b+c>0;③4a-2x+c>0;④当x>1时,y随着x的增大而增大.正确的说法个数是( )
(2013•平遥县模拟)如图是二次函数y=ax2+bx+c的图象,在下列说法中:①abc>0;②a+b+c>0;③4a-2x+c>0;④当x>1时,y随着x的增大而增大.正确的说法个数是( ) (2013•平遥县模拟)如图,在平面直角坐标系中,∠AOB=30°,点A坐标为(2,0).过A作AA1⊥OB,垂足为A1;过A1作A1A2⊥x轴,垂足为A2;再过点A2作A2A3⊥OB,垂足为点A3;再过点A3作A3A4⊥x轴,垂足为A4…;这样一直作下去,则A2013的纵坐标为
(2013•平遥县模拟)如图,在平面直角坐标系中,∠AOB=30°,点A坐标为(2,0).过A作AA1⊥OB,垂足为A1;过A1作A1A2⊥x轴,垂足为A2;再过点A2作A2A3⊥OB,垂足为点A3;再过点A3作A3A4⊥x轴,垂足为A4…;这样一直作下去,则A2013的纵坐标为