题目内容
【题目】如图,平行四边形![]() 的对角线
的对角线![]() 、
、![]() 相交于点O,
相交于点O,![]() .
.
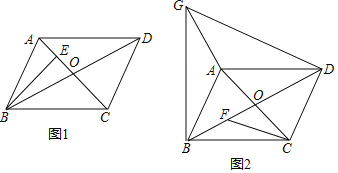
(1)如图1,过B作![]() 于E,若
于E,若![]() ,
,![]() ,求
,求![]() 的长;
的长;
(2)如图2,若![]() ,过点C作
,过点C作![]() 交
交![]() 于点F,过点B作
于点F,过点B作![]() 且
且![]() ,连接
,连接![]() .求证:
.求证:![]() .
.
【答案】(1)![]() -4;(2)见解析.
-4;(2)见解析.
【解析】
(1)由勾股定理可求CE的长,由平行四边形的性质可得CO的长,即可求OE的长;
(2)延长CF交AB于点H,由“SAS”可证△ABG≌△FCB,可得AG=BF,由等腰三角形的性质可得AB=CD=2BH,再证明三角形BFH为等腰直角三角形,从而得出BF=![]() BH①;在Rt△CDF中,得出DF=
BH①;在Rt△CDF中,得出DF=![]() CD=
CD=![]() AB=2
AB=2![]() BH,继而得出OF=BO-BF=
BH,继而得出OF=BO-BF=![]() BH②,结合①②可得出结论.
BH②,结合①②可得出结论.
(1)解:∵BC=AC=8,BE=5,![]() ,
,
∴CE=![]() .
.
∵四边形ABCD是平行四边形,
∴AO=CO=4,
∴OE=EC-OC=![]() -4;
-4;
(2)证明:如图,延长CF交AB于点H,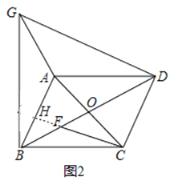
∵CF⊥CD,∠BDC=45°,
∴∠BDC=∠DFC=45°,
∴∠FBC+∠FCB=45°,CF=CD,
∵BC⊥BG,∠ABD=∠BDC=45°,
∴∠GBA+∠FBC=45°,
∴∠ABG=∠BCF,且AB=CD=CF,BC=BG,
∴△ABG≌△FCB(SAS),
∴AG=BF.
∵∠ABG+∠ABC=90°,∴∠BCF+∠ABC=90°,
∴CH⊥AB,又AC=BC,∴BH=AH,∴AB=CD=2BH.
∵AB∥CD,
∴∠ABF=∠CDB=45°,
∴∠HBF=∠BFH=45°,∴BH=FH,
∴BF=![]() BH①.
BH①.
在Rt△CDF中,CD=CF,∴DF=![]() CD=
CD=![]() AB=2
AB=2![]() BH,
BH,
∴BD=BF+DF=![]() BH +2
BH +2![]() BH=3
BH=3![]() BH,
BH,
∴BO=![]() BD=
BD=![]() BH,
BH,
∴OF=BO-BF=![]() BH②,
BH②,
∴由①②得,BF=2OF,
∴AG=2OF.

练习册系列答案
相关题目