题目内容
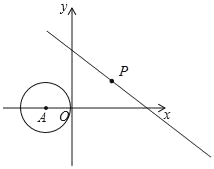
【题目】如图,在直角坐标系中,⊙A的圆心A的坐标为(﹣1,0),半径为1,点P为直线y=﹣![]() x+3上的动点,过点P作⊙A的切线,切点为Q,则切线长PQ的最小值是( )
x+3上的动点,过点P作⊙A的切线,切点为Q,则切线长PQ的最小值是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
【答案】C
【解析】
如图1,连接AP、AQ,根据切线的性质得AQ⊥PQ,则利用勾股定理得到PQ=![]() ,则当AP最小时,PQ最小,如图2,直线y=-
,则当AP最小时,PQ最小,如图2,直线y=-![]() x+3与y轴交于B,与x轴交于点C,则B(0,3),C(4,0),BC=5,利用垂线段最短得到当AP⊥BC于P时,AP最小,利用面积法可计算出AP=3,从而得到PQ的最小值.
x+3与y轴交于B,与x轴交于点C,则B(0,3),C(4,0),BC=5,利用垂线段最短得到当AP⊥BC于P时,AP最小,利用面积法可计算出AP=3,从而得到PQ的最小值.
如图1,连接AP、AQ,
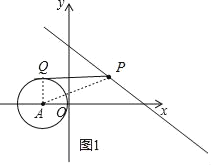
∵PQ为切线,
∴AQ⊥PQ,
在Rt△APQ中,PQ=![]() =
=![]() ,
,
当AP最小时,PQ最小,
如图2,直线y=﹣![]() x+3与y轴交于B,与x轴交于点C,则B(0,3),C(4,0),
x+3与y轴交于B,与x轴交于点C,则B(0,3),C(4,0),
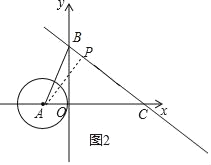
∴BC=![]() =5,
=5,
当AP⊥BC于P时,AP最小,
∵![]() APBC=
APBC=![]() BOAC,
BOAC,
∴AP=![]() =3,
=3,
∴PQ的最小值为![]() =2
=2![]() .
.
故选C.

【题目】在元旦期间,某商场计划购进甲、乙两种商品.
(1)已知甲、乙两种商品的进价分别为30元,70元,该商场购进甲、乙两种商品共50件需要2300元,则该商场购进甲、乙两种商品各多少件?
(2)该商场共投入9500元资金购进这两种商品若干件,这两种商品的进价和售价如表所示:
甲 | 乙 | |
进价(元/件) | 30 | 70 |
售价(元/件) | 50 | 100 |
若全部销售完后可获利5000元(利润=(售价﹣进价)×销量),则该商场购进甲、乙两种商品各多少件?
【题目】为了进一步了解八年级学生的身体素质情况,体育老师以八年级(1)班50位学生为样本进行了一分钟跳绳次数测试.根据测试结果,绘制出部分频数分布表和部分频数分布直方图.
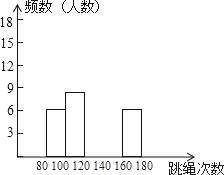
组别 | 次数x | 频数(人数) |
第1组 | 80≤x<100 | 6 |
第2组 | 100≤x<120 | 8 |
第3组 | 120≤x<140 | a |
第4组 | 140≤x<160 | 18 |
第5组 | 160≤x<180 | 6 |
请结合图表完成下列问题:
(1)表中的a= ;
(2)请把频数分布直方图补充完整;
(3)这个样本数据的中位数落在第 组;
(4)已知该校八年级共有学生800,请你估计一分钟跳绳次数不低于120次的八年级学生大约多少名?