题目内容
如图，⊙O1与⊙O2相交于点A、B，且AO1、AO2分别是两圆的切线，A是切点，若⊙O1的半径r1=3cm，⊙O2的半径r2=4cm，则弦AB=________cm．
分析：根据切线的性质得到直角三角形，再根据勾股定理求得O1O2的长；
根据相交两圆的性质，得到AB⊥O1O2，从而再根据三角形的面积即可求解．
解答：∵AO1、AO2分别是两圆的切线，
∴AO1⊥AO2．
∵⊙O1的半径r1=3cm，⊙O2的半径r2=4cm，
∴O1O2=5，
根据相交两圆的性质，得到AB⊥O1O2，
则AB=2×
=（cm）．点评：此题综合运用了切线的性质、勾股定理、相交两圆的性质和直角三角形斜边上的高等于两条直角边的乘积除以斜边的结论．
练习册系列答案
口算题天天练系列答案
相关题目
12、已知：如图，⊙O1与⊙O2外切于点P，直线AB过点P交⊙O1于A，交⊙O2于B，点C、D分别为⊙O1、⊙O2上的点，且∠ACP=65°，则∠BDP=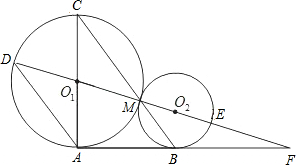
已知：如图，⊙O1与⊙O2外切于M点，AF是两圆的外公切线，A、B是切点，DF经过O1、O2，分别交⊙O1于D、⊙O2于E，AC是⊙O1的直径，BC经过M点，连接AD．
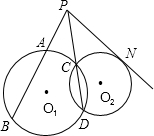如图，⊙O1与⊙O2相交于C、D两点，⊙O1的割线PAB与DC的延长线交于点P，PN与⊙O2相切于点N，若PB=10，AB=6，则PN=
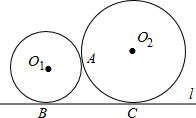已知：如图，⊙O1与⊙O2外切于A点，直线l与⊙O1、⊙O2分别切于B，C点，若⊙O1的半径r1=2cm，⊙O2的半径r2=3cm．求BC的长．
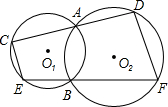已知如图：⊙O1与⊙O2相交于AB两点，过点A、B的直线分别与⊙O1交于C、E，与⊙O2交于D、F，连接CE、DF．