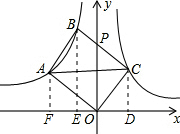
题目内容
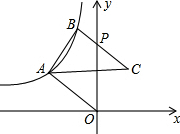 如图:已知反比例函数
如图:已知反比例函数 (x<0)和
(x<0)和 (x>0),直线OA与双曲线
(x>0),直线OA与双曲线 (x<0)交于A点,将直线OA向上平移使其分别交双曲线于B、C两点,与y轴交于P,且S△ABC=4,
(x<0)交于A点,将直线OA向上平移使其分别交双曲线于B、C两点,与y轴交于P,且S△ABC=4,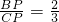 ,则k=________.
,则k=________.

分析:设A(xa,ya),B(xb,yb),C(xc,yc),则有xaya=xbyb=-2,xcyc=k,根据OA∥BC,可得
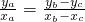 ,再由S△ABC=S梯形AFEB+S梯形BEDC-S梯形AFDC=4
,再由S△ABC=S梯形AFEB+S梯形BEDC-S梯形AFDC=4,可得yaxb-xayb+ybxc-ycxb-yaxc+xayc=8 ②,联立①②得:ybxc-ycxb=8 ③,再由
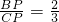 ,得
,得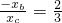 ,即xb=-
,即xb=- xc,代入可得出xcyc的值,即得出k的值.
xc,代入可得出xcyc的值,即得出k的值.解答:
 解:设A(xa,ya),B(xb,yb),C(xc,yc),则有xaya=xbyb=-2,xcyc=k.
解:设A(xa,ya),B(xb,yb),C(xc,yc),则有xaya=xbyb=-2,xcyc=k.由平移性质,可得OA∥BC,
∴
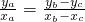 ,
,整理得:yaxb-yaxc=xayb-xayc ①
过点A作AF⊥x轴于点F,BE⊥x轴于点E,CD⊥x轴于点D.
∵S△ABC=S梯形AFEB+S梯形BEDC-S梯形AFDC=4
∴
 (AF+BE)•EF+
(AF+BE)•EF+ (BE+CD)•DE-
(BE+CD)•DE- (AF+CD)•DF=4,
(AF+CD)•DF=4,即:
 (ya+yb)•(xb-xa)+
(ya+yb)•(xb-xa)+ (yb+yc)•(xc-xb)-
(yb+yc)•(xc-xb)- (ya+yc)•(xc-xa)=4,
(ya+yc)•(xc-xa)=4,整理得:yaxb-xayb+ybxc-ycxb-yaxc+xayc=8 ②
由①②式得:ybxc-ycxb=8 ③
由
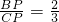 ,易得
,易得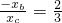 ,即xb=-
,即xb=- xc,
xc,∴yb=
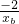 =
=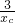 ,
,代入③式得:3+
 xcyc=8,
xcyc=8,∴xcyc=
 ,
,即k=
 .
.故答案为:
 .
.点评:本题考查了反比例函数的综合,涉及了平行线的性质,点的坐标与线段长度的转换及不规则面积的求解,解答本题的关键是数形结合思想及整体代入思想的运用,难度较大.

练习册系列答案
 中考解读考点精练系列答案
中考解读考点精练系列答案
相关题目
 如图,已知反比例函数
如图,已知反比例函数 如图,已知反比例函数
如图,已知反比例函数 如图,已知反比例函数y=
如图,已知反比例函数y= 如图,已知反比例函数
如图,已知反比例函数 如图,已知反比例函数y=
如图,已知反比例函数y=