题目内容
(2012•清远一模)将抛物线y=x2-2x+1的图象绕它的顶点A旋转180°,则旋转后的抛物线的函数关系式为( )A.y=-x2+2x+1
B.y=-x2-2x+1
C.y=-x2+2x-1
D.y=x2+2x+1
【答案】分析:利用抛物线的平移性质解答即可.
解答:解:∵原抛物线的顶点为(1,0),抛物线y=x2-2x+1的图象绕它的顶点A旋转180°后开口方向将改变,
∴顶点坐标不再改变,所以a=-1,
新抛物线的顶点坐标为(1,0),可设旋转后的抛物线的函数关系式为y=-(x-h)2+k,
解得y=-(x-1)2,
整理得y=-x2+2x-1.
故选C.
点评:解决本题的关键是理解绕抛物线的顶点旋转180°得到新函数的二次项的系数符号改变,顶点不变.
解答:解:∵原抛物线的顶点为(1,0),抛物线y=x2-2x+1的图象绕它的顶点A旋转180°后开口方向将改变,
∴顶点坐标不再改变,所以a=-1,
新抛物线的顶点坐标为(1,0),可设旋转后的抛物线的函数关系式为y=-(x-h)2+k,
解得y=-(x-1)2,
整理得y=-x2+2x-1.
故选C.
点评:解决本题的关键是理解绕抛物线的顶点旋转180°得到新函数的二次项的系数符号改变,顶点不变.

练习册系列答案
相关题目
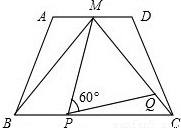
 ,∠CAD=30°.
,∠CAD=30°.