��Ŀ����
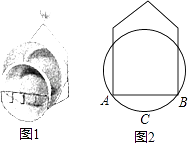
����Ŀ��ǭ������ijУ����ʦ��֯�ţ�1����ͬѧ��չ��ѧ�������ͬѧ�Dz���ѧУ����һ���߸˵ĸߣ���֪���߸�ֱ���ڵ����ϣ�ij����̫����������£����߸˵�Ӱ�ӣ�����BCD��ǡ������ˮƽ�����б���ϣ���D����õ��߸˶���A������Ϊ30�㣬��C����õ��߸˶���A������Ϊ45�㣬б��������60��ǣ�CD=4m�����������Щ��������߸˵ĸߣ�AB����
�������ȷ��1m���ο����ݣ� ![]() ��1.4��
��1.4�� ![]() ��1.7��
��1.7��
���𰸡��⣺�ӳ�AD��BC���ӳ�����G����DH��BG��H����ͼ��ʾ��
��Rt��DHC�У���DCH=60�㣬CD=4��
��CH=CDcos��DCH=4��cos60��=2��DH=CDsin��DCH=4��sin60��=2 ![]() ��
��
��DH��BG����G=30�㣬
��HG= ![]() =
= ![]() =6��
=6��
��CG=CH+HG=2+6=8��
��AB=xm��
��AB��BG����G=30�㣬��BCA=45�㣬
��BC=x��BG= ![]() =
= ![]() =
= ![]() x��
x��
��BG��BC=CG��
�� ![]() x��x=8��
x��x=8��
��ã�x��11��m����
�𣺵��߸˵ĸ�Ϊ11m��
�����������⿼����ǽ�ֱ�������ε�Ӧ�é����Ǹ������⣬�������Ǹ��ǵĸ�����������Ǻ����Ķ����ǽ���Ĺؼ����ӳ�AD��BC���ӳ�����G����DH��BG��H�������Ǻ���������CH��DH�ij����ó�CG����AB=xm���������еĶ������BG���ó����̣��ⷽ�̼��ɣ�

 С��ſ�ʱ��ҵϵ�д�
С��ſ�ʱ��ҵϵ�д� һ������ϵ�д�
һ������ϵ�д� �Ƹ�С״Ԫ���ֳ������ϵ�д�
�Ƹ�С״Ԫ���ֳ������ϵ�д� �¸��̵�ѧϵ�д�
�¸��̵�ѧϵ�д� ����ͬѧһ����ʦȫ�źþ�ϵ�д�
����ͬѧһ����ʦȫ�źþ�ϵ�д�