��Ŀ����
����Ŀ��Rt��ABC�У���ACB=90�㣬BC=4����ͼ1����P��C�������B�˶�����R������PB��һ�㣬PR=3CP������R��QR��BC����QR=aCP������PQ����P�㵽��B��ʱֹͣ�˶�����CP=x����ABC���PQR�غϲ��ֵ����ΪS��S����x�ĺ���ͼ����ͼ2��ʾ������0��x��![]() ��
�� ![]() ��x��m��m��x��nʱ�������Ľ���ʽ��ͬ����
��x��m��m��x��nʱ�������Ľ���ʽ��ͬ����
��1��a��ֵΪ��
��2�����S����x�ĺ�����ϵʽ����д��x��ȡֵ��Χ��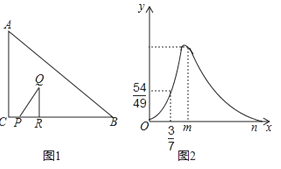
���𰸡��⣺��1����ͼ2��֪����x=![]() ʱ����Q���߶�AB�ϣ��Ҵ�ʱ��S=
ʱ����Q���߶�AB�ϣ��Ҵ�ʱ��S=![]() ��
��
PR=3CP=![]() ��QR=aCP=
��QR=aCP=![]() a��
a��
��QR��BC��
��S=![]() PRQR=
PRQR=![]() ��
��![]() ��
��![]() a=
a=![]() ����27a=108��
����27a=108��
���a=4��
��2����x=![]() ʱ��Q�����߶�AB�ϣ���ͼ3��
ʱ��Q�����߶�AB�ϣ���ͼ3��
��AC��BC��QR��BC��
��AC��QR��
���ABC�ס�QBR��
��![]()
QR=4CP=![]() ��PR=3CP=
��PR=3CP=![]() ��BR=BC��CP��PR=
��BR=BC��CP��PR=![]() ��
��
AC=![]() QR=
QR=![]()
![]() =3 ����
=3 ����
�ٵ���Q�ڡ�ACB��ʱ����0��x��![]() ʱ����ͼ1��
ʱ����ͼ1��
PR=3x��QR=4x��
S=![]() PRQR=6x2 ��
PRQR=6x2 ��
�ڵ���Q�ڡ�ACB����R�����߶�CB��ʱ����ͼ4��
��ʱx��![]() ����CR��BC��
����CR��BC��
��CR=CP+PR=4x��
��![]() ��x��1��
��x��1��
��![]()
���PQR�ס�ABC��
���Q=��B��
�ߡ�DEQ=��REB���Զ��ǣ���
���DEQ�ס�REB��
��Rt��ACB�У��ɹ��ɶ�����֪AB=![]() =5��
=5��
��AC��QR��
���EBR�ס�ABC��
��![]()
RB=BC��CP��PR=4��4x��AC=3��BC=4��
��RE=3��3x��
QE=QR��RE=4x����3��3x��=7x��3��
�ߡ�DEQ�ס�REB����EBR�ס�ABC����AC=3��BC=4��AB=5��
��DE=![]() QE��QD=
QE��QD=![]() QE��QD��DE��
QE��QD��DE��
S=![]() PRQR��
PRQR��![]() QDDE=��
QDDE=��![]() x2+
x2+![]() x��
x��![]() ��
��
�۵���R���߶�CB���ӳ�����ʱ����ͼ5��
��ʱCR=4x��BC=4����x��1��CP=x��BC=4��
��1��x��4��
�ߡ�ABC�ס�PQR��
���QPR=��A��
�ߡ�PBM=��ABC��
���PBM�ס�ABC��
��PM=![]() PB��MB=
PB��MB=![]() PB��
PB��
��PB=BC��CP=4��x��
�� S=![]() PMMB=
PMMB=![]() ��4��x��2=
��4��x��2=![]() x2��
x2��![]() x+
x+![]() ��
��
�ۺϢ٢ڢۿɵã�S=
����������1����ͼ2��֪��x=![]() ʱS=
ʱS=![]() �� �Ҵ�ʱQ�����߶�AB�ϣ����������������ʽ�������a��ֵ��
�� �Ҵ�ʱQ�����߶�AB�ϣ����������������ʽ�������a��ֵ��
��2����Q���R���λ�ã��ɽ������ƶ����̷ֳ������֣��������������ƣ��Ҹ����ߵĹ�ϵ���ָ�ͼ�Σ������ҳ�S��x֮��Ĺ�ϵʽ��