Question

【题目】已知：如图，∠MON在∠AOB的内部，点C、D分别在射线OA、OB上，且OC＝OD，CE⊥OA，DF⊥OB，分别交OM、ON于点E，F．

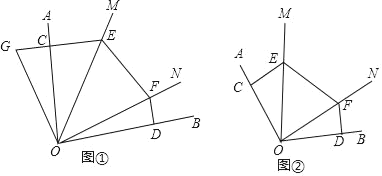
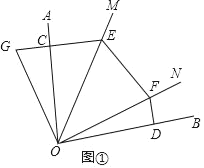
（1）如图①所示，若∠AOB＝90°，∠MON＝45°，延长EC至点G，使得CG＝DF．请证明EF＝CE+DF；

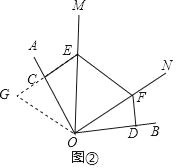
（2）如图②所示，若∠AOB＝115°，EF＝CE+DF，求∠MON的度数？

Answer 1

【答案】（1）详见解析；（2）∠MON＝57.5°

【解析】

（1）先证出△OCG≌△ODF（SAS），再证出△EOG≌△EOF（SAS），即可得：EF=CE+DF；
（2）仿照（1）的思路，延长EC至G，使CG=DF，连接OG，先证明：△OCG≌△ODF（SAS），再证明：△OEG≌△OEF（SSS），即可求得：∠MON=57.5°．

解：（1）如图①，

证明：∵CE⊥OA，DF⊥OB，

∴∠OCG＝∠ODF＝90°，

∵OC＝OD，CG＝DF．

∴△OCG≌△ODF（SAS）

∴∠COG＝∠DOF，OG＝OF

∵∠AOB＝90°，∠MON＝45°，

∴∠COE+∠DOF＝45°

∴∠COE+∠COG＝45°

即∠EOG＝45°＝∠MON

在△EOG≌△EOF中

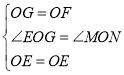
∴△EOG≌△EOF（SAS）

∴EF＝EG

即：EF＝CE+DF．

（2）如图②，延长EC至G，使CG＝DF，连接OG，

∵CE⊥OA，DF⊥OB，

∴∠OCG＝∠ODF＝90°，

∵OC＝OD，CG＝DF．

∴△OCG≌△ODF（SAS）

∴∠COG＝∠DOF，OG＝OF

∵EG＝CE+CG＝CE+DF，EF＝CE+DF，

∴EG＝EF

∵OE＝OE

∴△OEG≌△OEF（SSS）

∴∠EOG＝∠EOF

∵∠EOG+∠EOF＝∠COG+∠AOF＝∠DOF+∠AOF＝∠AOB＝115°

∴∠EOF＝∠AOB＝57.5°

即：∠MON＝57.5°