��Ŀ����
����Ŀ���ڳ��нεĺ���ѧϰ�У����Ǿ����ˡ�ȷ�������ı���ʽ�����ú���ͼ���о������ʩ�Ӧ�ú���������⡱��ѧϰ���̣��ڻ�����ͼ��ʱ������ͨ������ƽ�Ƶķ���������һ��İ�������Ĵ���ͼ������澭����ѧϰ���̣�����������������⣺�ں���y��![]() �У���x��0ʱ��y��1����x��2ʱ��y��
�У���x��0ʱ��y��1����x��2ʱ��y��![]() ��
��
��1�����⺯���ı���ʽ�� ����
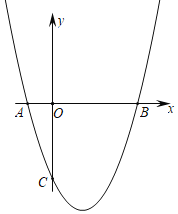
��2���ڸ�����ƽ��ֱ������ϵ�л�����������Ĵ���ͼ��д�����������һ�������� ����
��3������������ĺ���ͼ����y��![]() x+
x+![]() ��ͼ��ֱ��д������ʽ��
��ͼ��ֱ��д������ʽ��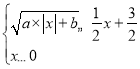 �Ľ⼯��
�Ľ⼯��
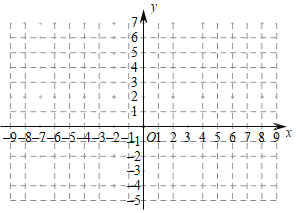
���𰸡���1��y��![]() ����2������y��Գƣ���3��0��x��1��
����2������y��Գƣ���3��0��x��1��
��������
��1�������ں���y��![]() �У���x��0ʱ��y��1����x��2ʱ��y��
�У���x��0ʱ��y��1����x��2ʱ��y��![]() ��������øú����ı���ʽ��
��������øú����ı���ʽ��
��2�����ݣ�1���еı���ʽ�б�����㣬���߿��Ի����ú�����ͼ�õ����������ʣ�
��3������ͼ�����ֱ��д������ʽ��Ľ⼯��
�����
�⣺��1�����ں���y��![]() �У���x��0ʱ��y��1����x��2ʱ��y��
�У���x��0ʱ��y��1����x��2ʱ��y��![]() ��
��
�� ����
����![]() ��
��
����������ı���ʽ��y��![]() ��
��
�ʴ�Ϊ��y��![]() ��
��
��2����y��![]() ��
��
��y�� ��
��
���
x | ��5 | ��2 | ��1 | 0 | 1 | 2 | 5 | �� |
y | 4 |
| 2 | 1 | 2 |
| 4 | �� |
��㡢�������ú�����ͼ����ͼ��ʾ��

���������ʣ�����y��Գƣ�
�ʴ�Ϊ������y��Գƣ�
��3����![]() ����ֱ�߸������ߣ���
����ֱ�߸������ߣ���![]() ��
��
���ɺ���ͼ��ɵã�����ʽ�� �Ľ⼯��0��x��1��
�Ľ⼯��0��x��1��


 ��ʦ�㲦��ϵ�д�
��ʦ�㲦��ϵ�д�