题目内容
已知等腰梯形的一条对角线与一腰垂直,上底与腰长相等,且上底的长度为1,则下底的长为________.
2
分析:根据平行线的性质和等腰三角形的性质推出∠ACB=∠DCA= ∠DCB,根据等腰梯形的性质得到∠B=∠DCB,根据三角形的内角和定理求出∠B=60°,∠ACB=30°,根据直角三角形的性质得出BC=2AB,代入求出即可.
∠DCB,根据等腰梯形的性质得到∠B=∠DCB,根据三角形的内角和定理求出∠B=60°,∠ACB=30°,根据直角三角形的性质得出BC=2AB,代入求出即可.
解答: 解:∵AD∥BC,
解:∵AD∥BC,
∴∠DAC=∠ACB,
∵AD=DC,
∴∠DAC=∠DCA,
∴∠ACB=∠DCA= ∠DCB,
∠DCB,
∵AD∥BC,AB=DC,
∴∠B=∠DCB,
∵AC⊥AB,
∴∠BAC=90°,
∴∠B+∠ACB=90°,
∴∠B=60°,∠ACB=30°,
∴BC=2AB=2×1=2,
故答案为:2.
点评:本题主要考查对等腰梯形的性质,三角形的内角和定理,等腰三角形的性质和判定,平行线的性质,含30度角的直角三角形的性质等知识点的理解和掌握,能综合运用这些性质进行计算是解此题的关键.
分析:根据平行线的性质和等腰三角形的性质推出∠ACB=∠DCA=
 ∠DCB,根据等腰梯形的性质得到∠B=∠DCB,根据三角形的内角和定理求出∠B=60°,∠ACB=30°,根据直角三角形的性质得出BC=2AB,代入求出即可.
∠DCB,根据等腰梯形的性质得到∠B=∠DCB,根据三角形的内角和定理求出∠B=60°,∠ACB=30°,根据直角三角形的性质得出BC=2AB,代入求出即可.解答:
 解:∵AD∥BC,
解:∵AD∥BC,∴∠DAC=∠ACB,
∵AD=DC,
∴∠DAC=∠DCA,
∴∠ACB=∠DCA=
 ∠DCB,
∠DCB,∵AD∥BC,AB=DC,
∴∠B=∠DCB,
∵AC⊥AB,
∴∠BAC=90°,
∴∠B+∠ACB=90°,
∴∠B=60°,∠ACB=30°,
∴BC=2AB=2×1=2,
故答案为:2.
点评:本题主要考查对等腰梯形的性质,三角形的内角和定理,等腰三角形的性质和判定,平行线的性质,含30度角的直角三角形的性质等知识点的理解和掌握,能综合运用这些性质进行计算是解此题的关键.

练习册系列答案
 新课标快乐提优暑假作业陕西旅游出版社系列答案
新课标快乐提优暑假作业陕西旅游出版社系列答案
相关题目
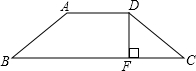 如图,等腰梯形ABCD中,AD=2,BC=6,高DF=2,则腰长DC=
如图,等腰梯形ABCD中,AD=2,BC=6,高DF=2,则腰长DC= 21、如图,已知?ABCD和?AB′C′D有一条公共边AD,它们的对边在同一条直线上.
21、如图,已知?ABCD和?AB′C′D有一条公共边AD,它们的对边在同一条直线上. 如图,已知?ABCD和?AB′C′D有一条公共边AD,它们的对边在同一条直线上.
如图,已知?ABCD和?AB′C′D有一条公共边AD,它们的对边在同一条直线上.