题目内容
若两个相似三角形的面积比为9:4,则这两个相似三角形的周长之比为( )
| A、2:3 | B、3:2 |
| C、4:9 | D、9:4 |
考点:相似三角形的性质
专题:
分析:由相似三角形的面积的比等于相似比的平方,可求得相似比;又由相似三角形(多边形)的周长的比等于相似比,即可求得答案.
解答:解:∵两个相似三角形的面积比为9:4,
∴这两个相似三角形的相似比为:3:2,
∴这两个相似三角形的周长之比为:3:2.
故选B.
∴这两个相似三角形的相似比为:3:2,
∴这两个相似三角形的周长之比为:3:2.
故选B.
点评:此题考查了相似三角形的性质.此题比较简单,注意熟记定理是解此题的关键.

练习册系列答案
相关题目
要求画△ABC的边AB上的高,下列画法中,正确的是( )
A、 |
B、 |
C、 |
D、 |
下面四个几何体中,其主视图不是中心对称图形的是( )
| A、圆柱 | B、圆锥 | C、球体 | D、正方体 |
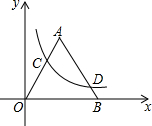 如图,若双曲线y=
如图,若双曲线y=