题目内容
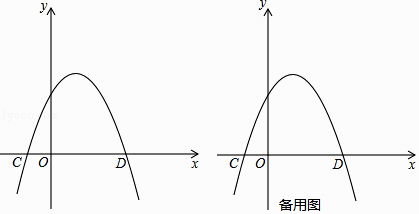
【题目】如图，已知抛物线y=ax2+ 
x+c与x轴交于A，B两点，与y轴交于丁C，且A（2，0），C（0，﹣4），直线l：y=﹣ 
x﹣4与x轴交于点D，点P是抛物线y=ax2+ x+c上的一动点，过点P作PE⊥x轴，垂足为E，交直线l于点F．
（1）
试求该抛物线表达式；
（2）如图（1），四边形PCOF是平行四边形，求P点的坐标；
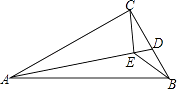
（3）如图（2），过点P作PH⊥y轴，垂足为H，连接AC．
①求证：△ACD是直角三角形；
②试问当P点横坐标为何值时，使得以点P、C、H为顶点的三角形与△ACD相似？
【答案】
（1）
解：由题意得： 
，解得：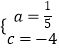 
，
∴抛物线的表达式为y= 
x2+ 
x﹣4．
（2）
解：设P（m， m2+ m﹣4），则F（m，﹣ 
m﹣4）．
∴PF=（﹣ m﹣4）﹣（ m2+ m﹣4）=﹣ m2﹣ 
m．
∵PE⊥x轴，
∴PF∥OC．
∴PF=OC时，四边形PCOF是平行四边形．
∴﹣ m2﹣ m=4，解得：m=﹣ 
或m=﹣8．
当m=﹣ 时， m2+ m﹣4=﹣ 
，
当m=﹣8时， m2+ m﹣4=﹣4．
∴点P的坐标为（﹣ ，﹣ ）或（﹣8，﹣4）．
（3）
解：①证明：把y=0代入y=﹣ x﹣4得：﹣ x﹣4=0，解得：x=﹣8．
∴D（﹣8，0）．
∴OD=8．
∵A（2，0），C（0，﹣4），
∴AD=2﹣（﹣8）=10．
由两点间的距离公式可知：AC2=22+42=20，DC2=82+42=80，AD2=100，
∴AC2+CD2=AD2．
∴△ACD是直角三角形，且∠ACD=90°．
②由①得∠ACD=90°．
当△ACD∽△CHP时， 
= 
，即 
= 
或 = 
，
解得：n=0（舍去）或n=﹣5.5或n=﹣10.5．
当△ACD∽△PHC时， = 
，即 = 
或即 = 
．
解得：n=0（舍去）或n=2或n=﹣18．
综上所述，点P的横坐标为﹣5.5或﹣10.5或2或﹣18时，使得以点P、C、H为顶点的三角形与△ACD相似．
【解析】（1）将点A和点C的坐标代入抛物线的解析式可得到关于a、c的方程组，然后解方程组求得a、c的值即可；（2）设P（m， m2+ m﹣4），则F（m，﹣ m﹣4），则PF=﹣ m2﹣ m，当PF=OC时，四边形PCOF是平行四边形，然后依据PF=OC列方程求解即可；（3）①先求得点D的坐标，然后再求得AC、DC、AD的长，最后依据勾股定理的逆定理求解即可；②分为△ACD∽△CHP、△ACD∽△PHC两种情况，然后依据相似三角形对应成比例列方程求解即可
【考点精析】根据题目的已知条件，利用相似三角形的应用的相关知识可以得到问题的答案，需要掌握测高：测量不能到达顶部的物体的高度，通常用“在同一时刻物高与影长成比例”的原理解决；测距：测量不能到达两点间的举例，常构造相似三角形求解．
