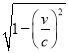��Ŀ����
����Ŀ����ͼ��������y=-x2+mx+n��x�ύ��A,B���㣬y���ύ�ڵ�C�������ߵĶԳ��ύx���ڵ�D����֪A(-1,0),C(0,3)
�������ߵĽ���ʽ��
�������ߵĶԳ������Ƿ����P�㣬ʹ�SPCD����CDΪ���ĵ��������Σ�������ڣ�ֱ��д����P�����꣬��������ڣ���˵�����ɣ�
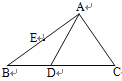
��E���߶�BC�ϵ�һ�����㣬����E��x��Ĵ������������ཻ�ڵ�F��
����ֱ��BC �Ľ���ʽ
�ڵ���E�˶���ʲôλ��ʱ���ı���CDBF�����������ı���CDBF������������ʱ��E������

���𰸡���1��y=��![]() x2+
x2+![]() x+2����2��P1��
x+2����2��P1��![]() ��4����P2��
��4����P2��![]() ��
�� ![]() ����P3��
����P3��![]() ����
����![]() ������3����y=��
������3����y=��![]() x+2����S�ı���CDBF��������=
x+2����S�ı���CDBF��������=![]() ��E��2��1��
��E��2��1��
�������������������1���ɴ���ϵ����������Ԫһ�η��������m��n��ֵ���ɣ�
��2����ͼ1�У��������������ۢٵ�PD=DCʱ����CP=CDʱ���ֱ�д����P���꼴�ɣ�
��3�������BC�Ľ���ʽ�������E�ĺ�����Ϊa�����ı���CDBF�����=S��BCD+S��CEF+S��BEF���S��a�Ĺ�ϵʽ���ɶ��κ��������ʾͿ���������ۣ�
�����������1����������y=-![]() x2+mx+n����A��-1��0����C��0��2����
x2+mx+n����A��-1��0����C��0��2����
��ã� 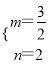 ��
��
�������ߵĽ���ʽΪ��y=-![]() x2+
x2+![]() x+2��
x+2��
��2����ͼ1��

��y=-![]() x2+
x2+![]() x+2��
x+2��
��y=-![]() ��x-
��x-![]() ��2+
��2+![]() ��
��
�������ߵĶԳ�����ֱ��x=![]() ��
��
��OD=![]() ��
��
��C��0��3����
��OC=23
��Rt��OCD�У��ɹ��ɶ�������CD=![]() ��
��
�ߡ�CDP����CDΪ���ĵ��������Σ�
��CP1=DP2=DP3��
��CH��x����H��
��HP1=HD=2��
��DP1=4��
��P1��![]() ��4����P2��
��4����P2��![]() ��
�� ![]() ����P3��
����P3��![]() ��-
��-![]() ����
����
��3����y=0ʱ��0=-![]() x2+
x2+![]() x+2
x+2
��x1=-1��x2=4��
��B��4��0����
��ֱ��BC�Ľ���ʽΪy=kx+b����ͼ��![]() ��
��
��ã� 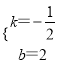 ��
��
��ֱ��BC�Ľ���ʽΪ��y=-![]() x+2��
x+2��
��ͼ2��

����C��CM��EF��M����E��a��-![]() a+2����F��a��-
a+2����F��a��-![]() a2+
a2+![]() a+2����
a+2����
��EF=-![]() a2+
a2+![]() a+2-��-
a+2-��-![]() a+2��=-
a+2��=-![]() a2+2a��0��x��4����
a2+2a��0��x��4����
��S�ı���CDBF=S��BCD+S��CEF+S��BEF=![]() BDOC+
BDOC+![]() EFCM+
EFCM+![]() EFBN��
EFBN��
=![]() ��
��![]() ��2+
��2+![]() a��-
a��-![]() a2+2a��+
a2+2a��+![]() ��4-a����-
��4-a����-![]() a2+2a����
a2+2a����
=-a2+4a+![]() ��0��x��4����
��0��x��4����
=-��a-2��2+![]()
��a=2ʱ��S�ı���CDBF��������=![]() ��
��
��E��2��1����