Question

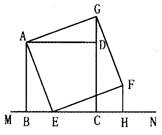
正方形四条边都相等，四个角都是90°，如图，已知正方形ABCD在直线MN的上方，BC在直线MN上，点E是BC上一点，以AE为边在BC所在的直线MN的上方作正方形AEFG．

(1)判断△ADG与△ABE是否全等，并说明理由；

(2)过点F作FH⊥MN，垂足为点H，观察并猜测线段FH与线段CH的数量关系，并说明理由．

 

Answer 1

【答案】

（1）△ADG≌△ABE．理由如下：

∵四边形ABCD和四边形AEFG是正方形，

∴AB=AD，AE=AG，∠ABE=∠ADG=90°，

∴∠BAE+∠EAD=∠DAG+∠EAD，

∴∠BAE=∠DAG．

∴△ADG≌△ABE；

（2）FH=CH．理由如下：

由已知可得∠EAG=∠BAD=∠AEF=90°，

由①得∠FEH=∠BAE=∠DAG，

又∵G在射线CD上，∠GDA=∠EHF=∠EBA=90°，AG=AE=EF，

∴∠BAE=∠DAG=∠EFH，

∴△EFH≌△GAD，△EFH≌△ABE，

∴EH=AD=BC，BE= FH

∴CH=BE．FH=CH

【解析】（1）利用正方形的性质及SAS定理求出△ADG≌△ABE，再利用全等三角形的性质即可解答；

（2）利用正方形的性质及SAS定理求出△ADG≌△ABE，再利用全等三角形的性质即可解答.