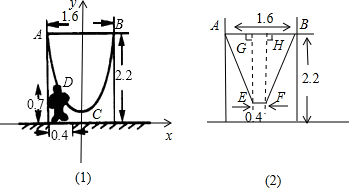
题目内容
抛物线y=
（x-3）2+2的顶点位于下列哪个函数的图象上（ ）A．y=3x+2
B．y=
C．y=3
D．y=-
【答案】分析：直接根据顶点式的特殊形式可得顶点坐标为（3，2），再把点（3，2）代入每一个函数式，逐一检验．
解答：解：因为y=
（x-3）2+2是抛物线的顶点式，顶点坐标为（3，2），当x=3时，
A、y=3x+2=3×3+2=11≠2，错误；
B、y=
x=
×3=2，正确；
C、y=3x=3×3=9，错误；
D、y=-
x=-
×3≠2，错误．
故选B．
点评：主要考查了求抛物线顶点坐标的方法和点在函数图象上的性质．
解答：解：因为y=
（x-3）2+2是抛物线的顶点式，顶点坐标为（3，2），当x=3时，A、y=3x+2=3×3+2=11≠2，错误；
B、y=
x=×3=2，正确；C、y=3x=3×3=9，错误；
D、y=-
x=-×3≠2，错误．故选B．
点评：主要考查了求抛物线顶点坐标的方法和点在函数图象上的性质．
练习册系列答案
怎样学好牛津英语系列答案
相关题目
A和C，和x轴的另一个交点为B．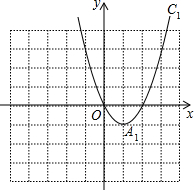
已知抛物线C1：y=x2-2x的图象如图所示，把C1的图象沿y轴翻折，得到抛物线C2的图象，抛物线C1与抛物线C2的图象合称图象C3．