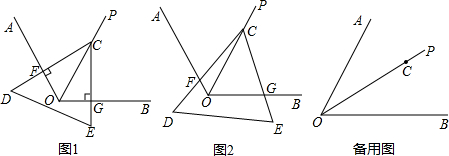
题目内容
已知△DCE的顶点C在ÐAOB的平分线OP上,CD交OA于F, CE交OB于G.
(1)如图1,若CD ^ OA, CE^ OB, 则图中有哪些相等的线段, 请直接写出你的结论:
;
(2)如图2, 若ÐAOB=120°, ÐDCE =ÐAOC, 试判断线段CF与线段CG的数量关系并
加以证明;
(3)若ÐAOB=a,当ÐDCE满足什么条件时,你在(2)中得到的结论仍然成立, 请
直接写出ÐDCE满足的条件.


解:(1)结论: CF=CG, OF=OG. ……………1分
 (2)法一:过点C作CM ^ OA于M,
CN^
OB于N.
(2)法一:过点C作CM ^ OA于M,
CN^
OB于N.
∵ OC平分ÐAOB,
∴ CM=CN, ÐCMF=ÐCNG=90°, ‚ …………2分
ÐAOC=ÐBOC.
∵ ÐAOB=120°,
∴ ÐAOC=ÐBOC=60°,
ÐMCN =360°-ÐAOB-ÐCMF-ÐCNO =60°.
∴ ÐDCE=ÐAOC =60°.
∴ ÐMCN=ÐFCG. …………………………………………3分
∴ ÐMCN -ÐFCN =ÐFCG -ÐFCN.
即 Ð1 =Ð2. ƒ …………………………………………4分
由 ‚ƒ 得△CMF≌△CNG.
∴ CF=CG. …………………………………………5分
法二:在OB上截取一点H, 使得OH=OC.
 ∵ OP平分ÐAOB, ÐAOB=120°,
∵ OP平分ÐAOB, ÐAOB=120°,
∴ Ð1=Ð2=60°, ÐDCE=Ð1=60°.
∵ OH=OC,
∴ △OCH是等边三角形.
∴ CO=CH, Ð2=Ð3 .
∴ Ð1=Ð3 . ‚ ……………………3分
∴ Ð4+Ð5=180°.
又 Ð5+Ð6=180°,
∴ Ð4=Ð6. ƒ …………………………………………4分
由 ‚ƒ 得△CFO≌△CGH.
∴ CF=CG. …………………………………………5分
(3) ÐDCE=180°- a 或OP平分ÐFCG . …………………………………………6分
【解析】略

 新课标阶梯阅读训练系列答案
新课标阶梯阅读训练系列答案