题目内容
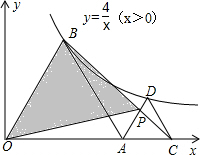 如图,△AOB和△ACD均为正三角形,且顶点B、D均在双曲线
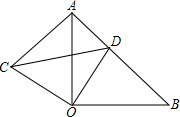
如图,△AOB和△ACD均为正三角形,且顶点B、D均在双曲线 (x>0)上,则图中S△OBP=
(x>0)上,则图中S△OBP=
- A.

- B.

- C.

- D.4
D
分析:先根据△AOB和△ACD均为正三角形可知∠AOB=∠CAD=60°,故可得出AD∥OB,所以S△ABP=S△AOP,故S△OBP=S△AOB,过点B作BE⊥OA于点E,由反比例函数系数k的几何意义即可得出结论.
解答: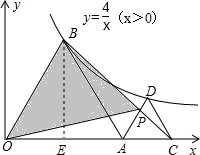 解:∵△AOB和△ACD均为正三角形,
解:∵△AOB和△ACD均为正三角形,
∴∠AOB=∠CAD=60°,
∴AD∥OB,
∴S△ABP=S△AOP,
∴S△OBP=S△AOB,
过点B作BE⊥OA于点E,则S△OBE=S△ABE= S△AOB,
S△AOB,
∵点B在反比例函数y= 的图象上,
的图象上,
∴S△OBE= ×4=2,
×4=2,
∴S△OBP=S△AOB=2S△OBE=4.
故选D.
点评:本题考查的是反比例函数综合题,涉及到等边三角形的性质及反比例函数系数k的几何意义等知识,难度适中.
分析:先根据△AOB和△ACD均为正三角形可知∠AOB=∠CAD=60°,故可得出AD∥OB,所以S△ABP=S△AOP,故S△OBP=S△AOB,过点B作BE⊥OA于点E,由反比例函数系数k的几何意义即可得出结论.
解答:
 解:∵△AOB和△ACD均为正三角形,
解:∵△AOB和△ACD均为正三角形,∴∠AOB=∠CAD=60°,
∴AD∥OB,
∴S△ABP=S△AOP,
∴S△OBP=S△AOB,
过点B作BE⊥OA于点E,则S△OBE=S△ABE=
 S△AOB,
S△AOB,∵点B在反比例函数y=
 的图象上,
的图象上,∴S△OBE=
 ×4=2,
×4=2,∴S△OBP=S△AOB=2S△OBE=4.
故选D.
点评:本题考查的是反比例函数综合题,涉及到等边三角形的性质及反比例函数系数k的几何意义等知识,难度适中.

练习册系列答案
相关题目
 15、如图,∠AOB和一条定长线段a,在∠AOB内找一点P,使P到OA,OB的距离都等于a,做法如下:
15、如图,∠AOB和一条定长线段a,在∠AOB内找一点P,使P到OA,OB的距离都等于a,做法如下: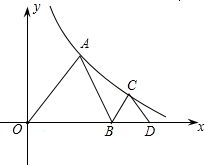 如图,△AOB和△BCD都是等边三角形,点A、C在函数
如图,△AOB和△BCD都是等边三角形,点A、C在函数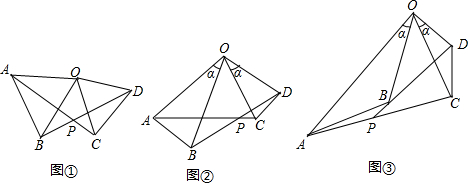
 如图,△AOB和△COD均为等腰直角三角形,∠AOB=∠COD=90°,D在AB上.
如图,△AOB和△COD均为等腰直角三角形,∠AOB=∠COD=90°,D在AB上. 如图,∠AOB和∠AOD分别是∠AOC的余角和补角,且OC是∠BOD的平分线,求∠AOC的度数.
如图,∠AOB和∠AOD分别是∠AOC的余角和补角,且OC是∠BOD的平分线,求∠AOC的度数.