题目内容
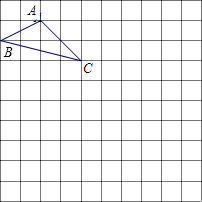 如图,在10×10的方格纸中,有一格点三角形ABC.(说明:顶点都在网格线交点处的三角形叫做格点三角形)
如图,在10×10的方格纸中,有一格点三角形ABC.(说明:顶点都在网格线交点处的三角形叫做格点三角形)(1)将△ABC先向右平移5格再向下平移2格,画出平移后的△A′B′C′;
(2)求点A到BC的距离;
(3)在所给的方格纸中,画一个与△ABC相似、且面积为6个平方单位的格点△DEF.
分析:(1)分别找出平移后的对应的点A′、B′、C′的位置,然后顺次连接即可得到△A′B′C′;
(2)把△ABC放到矩形里面,利用矩形的面积减去四周三个小三角形的面积,求出△ABC的面积,然后再求出BC的长度,根据三角形的面积即可求出点A到BC的距离;
(3)求出△DEF与△ABC的面积比等于2,根据相似三角形的面积比等于相似比的平方,所以△DEF的三边与△ABCD的三边的比为
即可.
(2)把△ABC放到矩形里面,利用矩形的面积减去四周三个小三角形的面积,求出△ABC的面积,然后再求出BC的长度,根据三角形的面积即可求出点A到BC的距离;
(3)求出△DEF与△ABC的面积比等于2,根据相似三角形的面积比等于相似比的平方,所以△DEF的三边与△ABCD的三边的比为
| 2 |
解答: 解:(1)如图,△A′B′C′就是△ABC先向右平移5格再向下平移2格得到的三角形;
解:(1)如图,△A′B′C′就是△ABC先向右平移5格再向下平移2格得到的三角形;
(2)设点A到BC的距离为x,根据题意BC=
=
,
∵S△ABC=4×2-
×2×1-
×1×4-
×2×2,
=8-1-2-2,
=3,
∴
×BC×x=3,
即
×
x=3,
解得x=
,
即点A到BC的距离是
;
(3)∵△DEF的面积是6个方格单位,△ABC的面积是3个方格单位,
∴S△DEF:S△ABC=2:1,
∴它们的边长的比=
:1,
根据网格AB=
=
,
BC=
=
,
AC=
=2
,
∴DE=
AB=
,
EF=
BC=
,
DF=
AC=4,
∴作出三边分别为
,
,4的△DEF就是所要求作的三角形.
故△DEF就是所要求作的三角形.
 解:(1)如图,△A′B′C′就是△ABC先向右平移5格再向下平移2格得到的三角形;
解:(1)如图,△A′B′C′就是△ABC先向右平移5格再向下平移2格得到的三角形;(2)设点A到BC的距离为x,根据题意BC=
| 42+12 |
| 17 |
∵S△ABC=4×2-
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
=8-1-2-2,
=3,
∴
| 1 |
| 2 |
即
| 1 |
| 2 |
| 17 |
解得x=
6
| ||
| 17 |
即点A到BC的距离是
6
| ||
| 17 |
(3)∵△DEF的面积是6个方格单位,△ABC的面积是3个方格单位,
∴S△DEF:S△ABC=2:1,
∴它们的边长的比=
| 2 |
根据网格AB=
| 12+22 |
| 5 |
BC=
| 12+42 |
| 17 |
AC=
| 22+ 22 |
| 2 |
∴DE=
| 2 |
| 10 |
EF=
| 2 |
| 34 |
DF=
| 2 |
∴作出三边分别为
| 10 |
| 34 |
故△DEF就是所要求作的三角形.
点评:本题考查了利用平移作图,根据三角形的面积求高,以及相似三角形面积的比等于相似比的平方的性质,难度中等.

练习册系列答案
相关题目
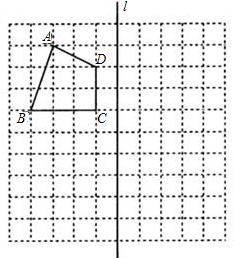
 形顶点上,且点A与原点重合.
形顶点上,且点A与原点重合. (2009•滨湖区一模)如图,在10×10的正方形网格中(每个小正方形的边长都为1个单位),△ABC的三个顶点都在格点上.
(2009•滨湖区一模)如图,在10×10的正方形网格中(每个小正方形的边长都为1个单位),△ABC的三个顶点都在格点上. 如图,在10×10的正方形网格中(每个小正方形的边长都为1个单位),△ABC的三个顶点都在格点上.
如图,在10×10的正方形网格中(每个小正方形的边长都为1个单位),△ABC的三个顶点都在格点上.