题目内容
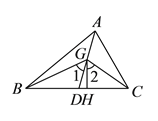
【题目】如图,在![]() 中,
中, ![]() 是它的角平分线,
是它的角平分线, ![]() 是
是![]() 上的一点,
上的一点, ![]() ,
, ![]() 分别平分
分别平分![]() ,
, ![]() ,
, ![]() ,垂足为点
,垂足为点![]() .
.
求证:( ![]() )
)![]() .(
.(![]() )
)![]() .
.
【答案】见解析.
【解析】试题分析:(1)由三角形内角和定理可知∠ABC+∠ACB=180°﹣∠BAC,然后利用角平分线的性质即可求出∠BGC=90°+![]() ∠BAC.
∠BAC.
(2)由AD是角平分线,得到∠BAD=∠CAD,然后根据图形可知:∠1=∠BAD+∠ABG,∠2=90°﹣∠GCH,最后根据三角形的内角和定理以及外角的性质即可求出答案.
试题解析:解:(1)由三角形内角和定理可知:∠ABC+∠ACB=180°﹣∠BAC.∵BG,CG分别平分∠ABC,∠ACB,∠GBC=![]() ∠ABC,∠GCB=
∠ABC,∠GCB=![]() ∠ACB,∴∠GBC+∠GCB=
∠ACB,∴∠GBC+∠GCB=![]() (∠ABC+∠ACB)=
(∠ABC+∠ACB)=![]() (180°﹣∠BAC)=90°﹣
(180°﹣∠BAC)=90°﹣![]() ∠BAC,∴∠BGC=180°﹣(∠GBC+∠GCB)=180°﹣
∠BAC,∴∠BGC=180°﹣(∠GBC+∠GCB)=180°﹣![]() (∠ABC+∠ACB)=90°+
(∠ABC+∠ACB)=90°+![]() ∠BAC;
∠BAC;
(2)∵AD是它的角平分线,∴∠BAD=∠CAD,∴∠1=∠BAD+∠ABG.∵GH⊥BC,∴∠GHC=90°,∴∠2=90°﹣∠GCH=90°﹣![]() ∠ACB=90°﹣
∠ACB=90°﹣![]() (180°﹣∠DAC﹣∠ADC)
(180°﹣∠DAC﹣∠ADC)
=![]() ∠DAC+
∠DAC+![]() ∠ADC.
∠ADC.
∵∠ADC=∠ABC+∠BAD,∴ ![]() ∠ADC=
∠ADC=![]() ∠ABC+∠
∠ABC+∠![]() ∠BAD=∠ABG+
∠BAD=∠ABG+![]() ∠BAD,∴∠2=
∠BAD,∴∠2=![]() ∠DAC+
∠DAC+![]() ∠ADC=
∠ADC=![]() ∠BAD+
∠BAD+![]() ∠BAD+∠ABG=∠BAD+∠ABG,∴∠1=∠2.
∠BAD+∠ABG=∠BAD+∠ABG,∴∠1=∠2.

【题目】某水果商行计划购进A、B两种水果共200箱,这两种水果的进价、售价如下表所示:
价格 | 进价(元/箱) | 售价(元/箱) |
A | 60 | 70 |
B | 40 | 55 |
(1)若该商行进贷款为1万元,则两种水果各购进多少箱?
(2)若商行规定A种水果进货箱数不低于B种水果进货箱数的 ![]() ,应怎样进货才能使这批水果售完后商行获利最多?此时利润为多少?
,应怎样进货才能使这批水果售完后商行获利最多?此时利润为多少?



