题目内容
如图，∠AOB=30°，点P是∠AOB内部的一个点，点E、F分别是OA、OB上的动点，当△PEF周长取得最小值时，∠EPF的度数为考点：轴对称-最短路线问题
专题：
分析：要求∠EPF的度数，要在△EPF中进行，根据轴对称的性质和等腰三角形的性质找出与∠CPD的关系，利用已知∠AOB=30°可求出∠CPD，答案可得．
解答：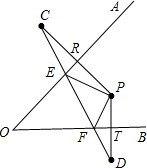
解：作P关于OA、OB的对称点C、D，连接CD角OA、OB于E、F．
此时△PEF周长有最小值；
∵P关于OA、OB的对称，
∴OA垂直平分PC，OB垂直平分PD，
∴CE=PE，PF=DF，
∴∠PEF=2∠C，∠PFE=2∠D，
∵∠PRE=∠PTF=90°，
∴在四边形OTPR中，
∴∠CPD+∠AOB=180°，
∵∠EPF+2∠C+2∠D=180°，
即∠CPD+∠C+∠D=180°，
∴∠C+∠D=∠AOB=30°
∴∠EPF=180°-30°×2=120°
故答案为120°．
解：作P关于OA、OB的对称点C、D，连接CD角OA、OB于E、F．此时△PEF周长有最小值；
∵P关于OA、OB的对称，
∴OA垂直平分PC，OB垂直平分PD，
∴CE=PE，PF=DF，
∴∠PEF=2∠C，∠PFE=2∠D，
∵∠PRE=∠PTF=90°，
∴在四边形OTPR中，
∴∠CPD+∠AOB=180°，
∵∠EPF+2∠C+2∠D=180°，
即∠CPD+∠C+∠D=180°，
∴∠C+∠D=∠AOB=30°
∴∠EPF=180°-30°×2=120°
故答案为120°．
点评：此题考查了轴对称的性质发现等腰三角形．在计算的过程中运用了四边形的内角和和三角形的内角和定理及其推论．
练习册系列答案
相关题目
已知ab＞0，
＜0，则下列结论正确的是（ ）
| c |
| b |
A、
| ||
| B、a＞c | ||
| C、a+b+c＞0 | ||
| D、ac＞0 |
某幼儿园的滑梯如图所示，已知滑梯长AC=10，BC=4，则此滑梯的坡角∠A的大小是
如图，BE与CD相交于点A，CF为∠BCD的平分线，EF为∠BED的角平分线，若∠B：∠D：∠F=2：4：x，求x的值．