题目内容
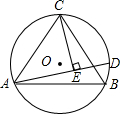 如图,等腰△ABC中,AC=BC,⊙O为△ABC的外接圆,D为
如图,等腰△ABC中,AC=BC,⊙O为△ABC的外接圆,D为 上一点,CE⊥AD于E,求证:AE=BD+DE.
上一点,CE⊥AD于E,求证:AE=BD+DE.
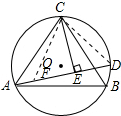 证明:如图,在AE上截取AF=BD,连接CF,CD;
证明:如图,在AE上截取AF=BD,连接CF,CD;在△ACF和△BCD中
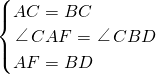
∴△ACF≌△BCD,
∴CF=CD,
∵CE⊥AD于E,
∴EF=DE,
∴AE=AF+EF=BD+DE.
分析:如图,在AE上截取AF=BD,连接CF,由圆周角定理得,∠CBD=∠CAF,根据SAS可以利用已知条件证明△ACF≌△BCD?CF=CD,由于CE⊥AD,根据等腰三角形的性质:底边上的高与底边上的中线重合知,EF=DE,则AE=AF+EF=BD+DE.
点评:本题通过作辅助线,构造全等三角形,利用圆周角定理和全等三角形的判定和性质及等腰三角形的性质求解.

练习册系列答案
相关题目
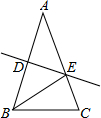 如图,等腰△ABC中,AB=AC,∠A=20°.线段AB的垂直平分线交AB于D,交AC于E,连接BE,则∠CBE等于( )
如图,等腰△ABC中,AB=AC,∠A=20°.线段AB的垂直平分线交AB于D,交AC于E,连接BE,则∠CBE等于( )| A、80° | B、70° | C、60° | D、50° |
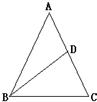 13、如图,等腰△ABC中,AB=AC,BD为腰AC的中线,将△ABC分成长12cm和9cm的两段,则等腰△ABC的腰长为
13、如图,等腰△ABC中,AB=AC,BD为腰AC的中线,将△ABC分成长12cm和9cm的两段,则等腰△ABC的腰长为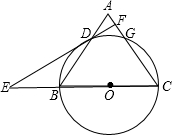 如图,等腰△ABC中,AC=BC=10,AB=12,以BC为直径作⊙0交AB于D,交AC于G,DF⊥AC,垂足为F,交CB的延长线于点E,则sinE=
如图,等腰△ABC中,AC=BC=10,AB=12,以BC为直径作⊙0交AB于D,交AC于G,DF⊥AC,垂足为F,交CB的延长线于点E,则sinE= 如图,等腰△ABC中,AB=AC,D为BC中点,E为射线AD上一点.
如图,等腰△ABC中,AB=AC,D为BC中点,E为射线AD上一点. 如图,等腰△ABC中,AB=AC,D、E分别为AC、AB的中点.
如图,等腰△ABC中,AB=AC,D、E分别为AC、AB的中点.