题目内容
如图，点B在DC上，BE平分∠ABD，∠DBE=∠A，你能判断BE与AC的位置关系吗？请说明理由．
解：BE∥AC．理由：
∵BE平分∠ABD，
∴∠DBE=∠ABE；
∵∠DBE=∠A，
∴∠ABE=∠A，
∴BE∥AC．
分析：欲证BE∥AC，在图中发现BE、AC被直线AB所截，且已知BE平分∠ABD，∠DBE=∠A，故可按内错角相等两直线平行判断．
点评：解答此类要判定两直线平行的题，可围绕截线找同位角、内错角和同旁内角．只有同位角相等、内错角相等、同旁内角互补，才能推出两被截直线平行．
∵BE平分∠ABD，
∴∠DBE=∠ABE；
∵∠DBE=∠A，
∴∠ABE=∠A，
∴BE∥AC．
分析：欲证BE∥AC，在图中发现BE、AC被直线AB所截，且已知BE平分∠ABD，∠DBE=∠A，故可按内错角相等两直线平行判断．
点评：解答此类要判定两直线平行的题，可围绕截线找同位角、内错角和同旁内角．只有同位角相等、内错角相等、同旁内角互补，才能推出两被截直线平行．
练习册系列答案
世纪百通主体课堂小学课时同步达标系列答案
世纪百通优练测系列答案
相关题目
24、如图，点B在DC上，BE平分∠ABD，∠DBE=∠A，你能判断BE与AC的位置关系吗？请说明理由．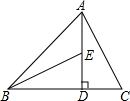
。事实上，在任何一个直角三角形中，两条直角边的平方之和一定等于斜边的平方。如果直角三角形中，两直角边长分别为a、b，斜边长为c，则
,这个结论就是著名的勾股定理．
的正整数组(a,b,c)叫勾股数组。例如(3,4,5)就是一组勾股数组。观察下列几组勾股数
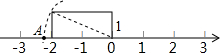
的B点（保留作图痕迹）．