题目内容
已知:如图,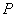 是
是 外一点,过点
外一点,过点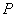 引圆的切线
引圆的切线 (
( 为切点)和割线
为切点)和割线 ,分别交
,分别交 于
于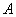 、
、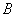 ,连接
,连接 、
、 。
。
(1)求证: ;
;
(2)利用(1)的结论,已知 ,
, ,求
,求 的长。
的长。

练习册系列答案
 各地期末复习特训卷系列答案
各地期末复习特训卷系列答案 小博士期末闯关100分系列答案
小博士期末闯关100分系列答案
相关题目
题目内容
已知:如图,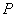 是
是 外一点,过点
外一点,过点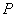 引圆的切线
引圆的切线 (
( 为切点)和割线
为切点)和割线 ,分别交
,分别交 于
于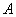 、
、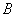 ,连接
,连接 、
、 。
。
(1)求证: ;
;
(2)利用(1)的结论,已知 ,
, ,求
,求 的长。
的长。

 各地期末复习特训卷系列答案
各地期末复习特训卷系列答案 小博士期末闯关100分系列答案
小博士期末闯关100分系列答案