Question

如图，C是的中点，CF⊥AB，F为垂足．
（1）求证：△AEC是等腰三角形．
（2）设AB=4，∠DAB=30°，求CE的长．

Answer 1

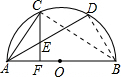解：（1）连接BC，
∵C是的中点，
∴∠CAD=∠ABC，
又∵AB是直径，
∴∠ACB=90°，又CF⊥AB，
∴∠ACF=∠ABC，
∴∠CAD=∠ACF，
∴△AEC是等腰三角形；

（2）连接BD，
在Rt△ABD中，∠DAB=30°，AB=4，则BD=2，
设∠CAD=∠ACF=x，
∴∠DAB+2x=90°，
∴2x=60°，即∠CAB=60°，∴CBA=30°，
∴AC=AB=2，
，∴AC=BD=2，
在△ACF中，AF=AC=1，
∴AE=，
∴CE=．
分析：（1）连接BC，根据圆周角定理得出∠ACB=90°，以及∠ACF=∠ABC，即可得出答案．
（2）根据在直角三角形中，30°角所对的直角边等于斜边的一半，得出AC=BD=2，进而得出AE的长即可．
点评：此题主要考查了圆周角定理以及等腰三角形的判定，根据已知作出辅助线构造直径所对圆周角是解题关键．