题目内容
如图(1),在锐角三角形ABC中,AB>BC>AC.D、E分别是AB、BC边上的两个动点,连接DE、CD.
(1)当点D、E运动时,分别在图(2)、图(3)中画出D.E运动的位置,要求在图(2)中,仅有一组三角形相似,在图(2)中,仅有两组三角形相似.
(2)当AB=9,BC=8,CA=6时,选择(1)中的图(3),即有两组三角形相似时,求DE的长.
(1)当点D、E运动时,分别在图(2)、图(3)中画出D.E运动的位置,要求在图(2)中,仅有一组三角形相似,在图(2)中,仅有两组三角形相似.
(2)当AB=9,BC=8,CA=6时,选择(1)中的图(3),即有两组三角形相似时,求DE的长.

分析:(1)作三角形相似,保证两角相等即可;
(2)利用相似三角形的性质解答.
(2)利用相似三角形的性质解答.
解答:解:(1)如图所示:

图(2)中仅有△ABC∽△ACD;
图(3)中仅有△ABC∽△ACD,△CBD∽△DBE;
(2)在图(3)中,由△ABC∽△ACD,得AD=
=4,CD=
=
∴BD=AB-AD=5.(1分)
由△CBD∽△DBE,得DE=
=
.

图(2)中仅有△ABC∽△ACD;
图(3)中仅有△ABC∽△ACD,△CBD∽△DBE;
(2)在图(3)中,由△ABC∽△ACD,得AD=
| AC2 |
| AB |
| BC•AC |
| AB |
| 16 |
| 3 |
∴BD=AB-AD=5.(1分)
由△CBD∽△DBE,得DE=
| CD•BD |
| BC |
| 10 |
| 3 |
点评:本题利用三角形相似的结论解题,考查了同学们的转化能力,解三角形问题往往用到相似.

练习册系列答案
 教材全解字词句篇系列答案
教材全解字词句篇系列答案
相关题目
 ∠MOB=
∠MOB=



 的度数是否改变?若不变,请求出
的度数是否改变?若不变,请求出

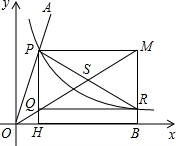
 的图象交于点P,以P为圆心、以2OP为半径作弧交图象于点R.分别过点P和R作x轴和y轴的平行线,两直线相交于点M,连接OM得到∠MOB,则∠MOB=
的图象交于点P,以P为圆心、以2OP为半径作弧交图象于点R.分别过点P和R作x轴和y轴的平行线,两直线相交于点M,连接OM得到∠MOB,则∠MOB= ∠AOB.要明白帕普斯的方法,请研究以下问题:
∠AOB.要明白帕普斯的方法,请研究以下问题: )、R(b,
)、R(b, ),求直线OM对应的函数表达式(用含a,b的代数式表示);
),求直线OM对应的函数表达式(用含a,b的代数式表示); ∠AOB;
∠AOB;