题目内容
【题目】已知抛物线![]() 的顶点坐标为
的顶点坐标为![]() 且经过点
且经过点![]() 动直线
动直线![]() 的解析式为
的解析式为![]()
![]() .
.
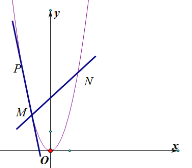
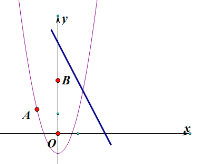
(1)求抛物线![]() 的解析式;
的解析式;
(2)将抛物线![]() 向上平移一个单位得到新的抛物线
向上平移一个单位得到新的抛物线![]() ,过点
,过点![]() 的直线交抛物线于
的直线交抛物线于![]() 两点(
两点(![]() 点位于
点位于![]() 点的左边),动直线
点的左边),动直线![]() 过点
过点![]() ,与抛物线
,与抛物线![]() 的另外一个交点为点
的另外一个交点为点![]() 求证:直线
求证:直线![]() 恒过一个定点;
恒过一个定点;
(3)已知点![]() ,且点
,且点![]() 在动直线
在动直线![]() 上,若
上,若![]() 是以
是以![]() 为顶角的等腰三角形,这样的等腰三角形有且只存在一个,请求出
为顶角的等腰三角形,这样的等腰三角形有且只存在一个,请求出![]() 的值.
的值.
【答案】(1)![]() ;(2)证明见解析;(3)
;(2)证明见解析;(3)![]() 或
或![]() .
.
【解析】
(1)先根据顶点坐标可设其解析式的顶点式,再将点![]() 代入求解即可;
代入求解即可;
(2)先根据二次函数图象的平移得到抛物线![]() 的解析式,设点M的坐标为
的解析式,设点M的坐标为![]() ,分别求出直线MN、动直线
,分别求出直线MN、动直线![]() 的解析式,然后分别联立两个一次函数与抛物线
的解析式,然后分别联立两个一次函数与抛物线![]() 的解析式,求出点P、N的坐标,最后利用待定系数法求出直线PN的解析式,由此即可得证;
的解析式,求出点P、N的坐标,最后利用待定系数法求出直线PN的解析式,由此即可得证;
(3)设点C的坐标为![]() ,先根据两点之间的距离公式求出AB、BC的长,再根据等腰三角形的定义得出
,先根据两点之间的距离公式求出AB、BC的长,再根据等腰三角形的定义得出![]() ,从而可得一个关于
,从而可得一个关于![]() 的一元二次方程,然后利用根的判别式求解即可.
的一元二次方程,然后利用根的判别式求解即可.
(1)![]() 抛物线
抛物线![]() 的顶点坐标为
的顶点坐标为![]()
![]() 可设抛物线
可设抛物线![]() 的解析式的顶点式为
的解析式的顶点式为![]()
将点![]() 代入得:
代入得:![]() ,解得
,解得![]()
故抛物线![]() 的解析式为
的解析式为![]() ;
;
(2)由题意得:抛物线![]() 的解析式为
的解析式为![]() ,即
,即![]()
设点M的坐标为![]()
设直线MN的解析式为![]()
将点![]() ,
,![]() 代入得
代入得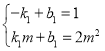 ,解得
,解得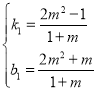
则直线MN的解析式为![]()
联立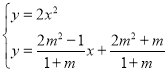
设点![]()
则![]() 是关于x的一元二次方程
是关于x的一元二次方程![]() 的两根
的两根
由根与系数的关系得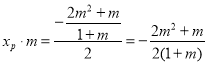
解得![]()
将![]() 代入抛物线
代入抛物线![]() 的解析式得:
的解析式得: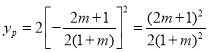
即![]()
将点![]() 代入
代入![]() 得
得![]() ,解得
,解得![]()
则动直线![]() 的解析式为
的解析式为![]()
联立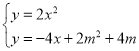
设点![]()
则![]() 是关于x的一元二次方程
是关于x的一元二次方程![]() 的两根
的两根
由根与系数的关系得![]()
解得![]()
将![]() 代入抛物线
代入抛物线![]() 的解析式得:
的解析式得:![]()
即![]()
设直线PN的解析式为![]()
将![]() 代入得:
代入得:![]()
将![]() 代入得:
代入得:![]()
解得
则直线PN的解析式为![]()
由此可知,当![]() 时,
时,![]()
即无论m取何值,直线PN恒过定点![]() ;
;
(3)设点C的坐标为![]()
![]()
![]() ,
,![]()
若![]() 是以
是以![]() 为顶角的等腰三角形,则
为顶角的等腰三角形,则![]() ,从而有
,从而有![]()
即![]()
整理得![]()
因为这样的等腰三角形有且只存在一个
所以关于![]() 的一元二次方程
的一元二次方程![]() 有两个相等的实数根
有两个相等的实数根
则此方程的根的判别式![]()
解得![]() 或
或![]() .
.

 习题精选系列答案
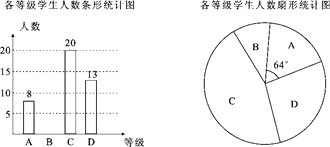
习题精选系列答案【题目】为争创文明城市,我市交警部门在全市范围开展了安全使用电瓶车专项宣传活动.在活动前和活动后分别随机抽取了部分使用电瓶车的市民,就骑电瓶车戴安全帽情况进行问卷调查,并将两次收集的数据制成如下统计图表.

类别 | 人数 | 百分比 |
A | 68 | 6.8% |
B | 245 | b% |
C | a | 51% |
D | 177 | 17.7% |
总计 | c | 100% |
根据以上提供的信息解决下列问题:
(1)a= ,b= c=
(2)若我市约有30万人使用电瓶车,请分别计算活动前和活动后全市骑电瓶车“都不戴”安全帽的人数.
(3)经过某十字路口,汽车无法继续直行只可左转或右转,电动车不受限制,现有一辆汽车和一辆电动车同时到达该路口,用画树状图或列表的方法求汽车和电动车都向左转的概率.