题目内容
 如图,对称轴为直线x=
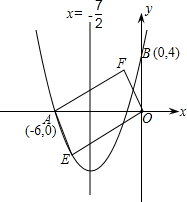
如图,对称轴为直线x=| 7 | 2 |
(1)求抛物线解析式及顶点D的坐标;
(2)设点E(x,y)是抛物线上位于第四象限内一动点,将△OAE绕OA的中点旋转180°,点E落到点F的位置.求四边形OEAF的面积S与x之间的函数关系式,并写出自变量x的取值范围;
①当四边形OEAF的面积为24时,请判断四边形OEAF的形状.
②是否存在点E,使四边形OEAF为正方形?若存在,求出点E的坐标;若不存在,请说明理由.
(3)若点P是x轴上一点,以P、A、D为顶点作平行四边形,该平行四边形的另一顶点在y轴上,请直接写出满足条件的所有点P的坐标.
分析:(1)已知抛物线的对称轴,可将其解析式设为顶点式,再根据已知的两点坐标由待定系数法确定该二次函数的解析式;进而能得到顶点D的坐标.
(2)将△OAE绕线段OA中点旋转180°后,旋转前后的两个三角形关于点OA的中点对称,所以四边形OEAF是平行四边形,在求该四边形的面积时,只需求出它的一半即△OAE的面积即可,以OA为底、点E的纵坐标的绝对值为高即可得到△OAE的面积表达式,则S、x的函数关系式可求;
①将S=24代入上面的S、x的函数关系式中,先求出点E的坐标,再判断四边形OEAF的形状;
②若四边形OEAF是正方形,那么△OAE必为等腰直角三角形,可据此求出点E的坐标,再代入抛物线的解析式中进行验证即可.
(3)此题需要分两种情况讨论(将平行四边形的另一顶点称作点Q):
①线段PA为对角线时,先求出DQ的中点,再由P、A关于这个中点对称来得到点P的坐标;
②线段PA为边时,那么DQ必与PA平行,即点Q、D的纵坐标相同,则DQ的长可知,而DQ=PA,可据此求出点P的坐标(注意在点A的左右两侧各有一个).
(2)将△OAE绕线段OA中点旋转180°后,旋转前后的两个三角形关于点OA的中点对称,所以四边形OEAF是平行四边形,在求该四边形的面积时,只需求出它的一半即△OAE的面积即可,以OA为底、点E的纵坐标的绝对值为高即可得到△OAE的面积表达式,则S、x的函数关系式可求;
①将S=24代入上面的S、x的函数关系式中,先求出点E的坐标,再判断四边形OEAF的形状;
②若四边形OEAF是正方形,那么△OAE必为等腰直角三角形,可据此求出点E的坐标,再代入抛物线的解析式中进行验证即可.
(3)此题需要分两种情况讨论(将平行四边形的另一顶点称作点Q):
①线段PA为对角线时,先求出DQ的中点,再由P、A关于这个中点对称来得到点P的坐标;
②线段PA为边时,那么DQ必与PA平行,即点Q、D的纵坐标相同,则DQ的长可知,而DQ=PA,可据此求出点P的坐标(注意在点A的左右两侧各有一个).
解答:解:(1)依题意,设抛物线的解析式为:y=a(x-
)2+h,代入A(6,0)、B(0,4)后,得:
,解得
∴抛物线的解析式:y=
(x-
)2-
,顶点D(
,-
).
(2)依题意,知:△OAF≌△AOE,得:OE=AF、AE=OF;
∴四边形OEAF是平行四边形.
∵点E(x,y)在抛物线的图象上,
∴y=
(x-
)2-
;
又∵点E在第四象限,∴y<0,解得:1<x<6;
S=2S△OAE=2•
•OA•|yE|=6•(-y)=-4(x-
)2+25,(1<x<6).
①当S=24时,-4(x-
)2+25=24,解得 x1=3、x2=4;
1、当x=3时,E(3,-4),此时OE=AE,四边形OEAF为菱形;
2、当x=4时,E(4,-4),此时OE≠AE,且∠OEA≠90°,∴四边形OEAF只是平行四边形.
②假设四边形OEAF为正方形,则OE=AE,OE⊥AE,已知O(0,0)、A(6,0),则 E(3,-3);
但此时的点E不在抛物线的图象上,因此不存在符合条件的点E.
(3)设平行四边形的另一顶点为Q,分两种情况讨论:
①当PA为平行四边形的对角线时,另一条对角线DQ的中点为(
,0),而P、A关于(
,0)对称,那么点P(-
,0);
②当PA为平行四边形的边时,DQ∥PA,且PA=QD=
,已知 A(6,0),则 P(
,0)或(
,0);
综上,点P的坐标为(-
,0)或(
,0)或(
,0).
| 7 |
| 2 |
|
|
∴抛物线的解析式:y=
| 2 |
| 3 |
| 7 |
| 2 |
| 25 |
| 6 |
| 7 |
| 2 |
| 25 |
| 6 |
(2)依题意,知:△OAF≌△AOE,得:OE=AF、AE=OF;
∴四边形OEAF是平行四边形.
∵点E(x,y)在抛物线的图象上,
∴y=
| 2 |
| 3 |
| 7 |
| 2 |
| 25 |
| 6 |
又∵点E在第四象限,∴y<0,解得:1<x<6;
S=2S△OAE=2•
| 1 |
| 2 |
| 7 |
| 2 |
①当S=24时,-4(x-
| 7 |
| 2 |
1、当x=3时,E(3,-4),此时OE=AE,四边形OEAF为菱形;
2、当x=4时,E(4,-4),此时OE≠AE,且∠OEA≠90°,∴四边形OEAF只是平行四边形.
②假设四边形OEAF为正方形,则OE=AE,OE⊥AE,已知O(0,0)、A(6,0),则 E(3,-3);
但此时的点E不在抛物线的图象上,因此不存在符合条件的点E.
(3)设平行四边形的另一顶点为Q,分两种情况讨论:
①当PA为平行四边形的对角线时,另一条对角线DQ的中点为(
| 7 |
| 4 |
| 7 |
| 4 |
| 5 |
| 2 |
②当PA为平行四边形的边时,DQ∥PA,且PA=QD=
| 7 |
| 2 |
| 5 |
| 2 |
| 19 |
| 2 |
综上,点P的坐标为(-
| 5 |
| 2 |
| 5 |
| 2 |
| 19 |
| 2 |
点评:此题主要考查了函数解析式的确定、图形的旋转、图形面积的求法以及特殊四边形的判定等知识;最后一题中,正确判断出最后一顶点的三种情况是解答题目的关键.

练习册系列答案
相关题目
 (2013•莒南县二模)如图,对称轴为直线x=
(2013•莒南县二模)如图,对称轴为直线x=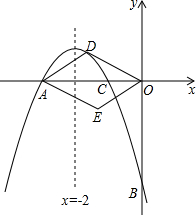 如图,对称轴为直线x=-2的抛物线经过A(-3,0)和B(0,-3).
如图,对称轴为直线x=-2的抛物线经过A(-3,0)和B(0,-3).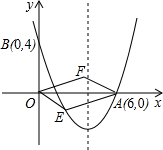 行四边形?若能,求出点E、F的坐标;若不能,请说明理由.(第(4)问不写解答过程,只写结论)
行四边形?若能,求出点E、F的坐标;若不能,请说明理由.(第(4)问不写解答过程,只写结论) 已知如图,对称轴为直线x=4的抛物线y=ax2+2x与x轴相交于点B、O.
已知如图,对称轴为直线x=4的抛物线y=ax2+2x与x轴相交于点B、O.