题目内容
如图10-1,已知AB是⊙O的直径,直线l与⊙O相切于点B,直线m垂直AB于点C,交⊙O于P、Q两点. 连结AP,过O作OD∥AP交l于点D,连接AD与m交于点M.
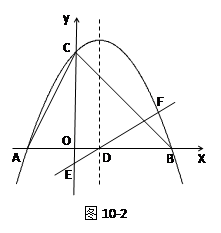
(1) 如图10-2,当直线m过点O时,求证:M是PO的中点;
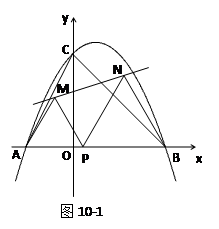
(2) 如图10-1,当直线m不过点O时,M是否仍为PC的中点?证明你的结论.

(1) 证明:连接PD,
∵ 直线m垂直AB于点C,直线l与⊙O相切于点B,AB为直径,
∴ ∠POA=∠DBA=90°.
又∵ AP∥OD,∴ ∠PAO=∠DOB.
又∵ AO=BO,∴ △APO≌△ODB.
∴ AP=OD,∴ 四边形APDO是平行四边形,
∴ M是PO的中点.
(其他解法:证△APO≌△ODB后,据中位线定理证![]() ;或证△DPO≌△DBO,得∠DPO=∠DBO=90°,从而证四边形APDO是平行四边形等.)
;或证△DPO≌△DBO,得∠DPO=∠DBO=90°,从而证四边形APDO是平行四边形等.)
(2) M是PC的中点. 证明如下:
∵AP∥OD,∴ ∠PAO=∠DOB,又 ∠PCA=∠DBO=90°,
∴ △APC∽△ODB,∴ ![]() .①
.①
又易证△ACM∽△ABD,∴ ![]() .
.
又∵ AB=2OB,∴ ![]() ,∴
,∴![]() .②
.②
由①②得,![]() ,∴ PC=2MC,即M是PC的中点.
,∴ PC=2MC,即M是PC的中点.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目


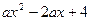 与x轴交于A、B两点,与y轴交于
与x轴交于A、B两点,与y轴交于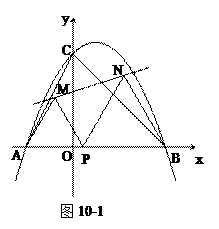

 与x轴交于A、B两点,与y轴交于
与x轴交于A、B两点,与y轴交于

 与x轴交于A、B两点,与y轴交于
与x轴交于A、B两点,与y轴交于
